ДВУЦЕНТРОВЫЕ ИНТЕГРАЛЫ ПЕРЕКРЫТИЯ – ЭТО ПРОСТО | Опубликовать статью РИНЦ

Баранов М.А.

Профессор, доктор физико-математических наук, Алтайский государственный технический университет

ДВУЦЕНТРОВЫЕ ИНТЕГРАЛЫ ПЕРЕКРЫТИЯ – ЭТО ПРОСТО

Аннотация

Интегралы по пространству от функций, аргументами которых являются радиусы-векторы, проведённые из двух заданных центров в произвольную точку являются ключевым понятием физической химии. Предложена схема, которая позволяет с требуемой точностью выполнить численное интегрирование двуцентровых функций без их разложения в ряд, применения рекуррентных соотношений и других приближённых методов. Двуцентровые интегралы от простых функций берутся аналитически.

Ключевые слова: атом, электронные оболочки, перекрывание, интегрирование.

Baranov M.A

Professor, PhD in Physics and mathematics, Altai State Technical University

TWO-CENTER OVERLAP INTEGRALS – IT IS SIMPLY

Abstract

Integrals on space of functions dependent on radiuses-vectors drawn from two given centers in any point are key concept of physical chemistry. Here the scheme is offered which allows at required precision execute numerical integration of two-centered functions without of their decomposition in series, resorting to recurrent relations and to other approached methods. In case of simple functions the scheme allows execute their integration analytically.

Key words: atom, electronic shells, overlapping, interaction.

Introduction

Practically all world around of us is based on interactions of bodies. In macro-scale these interactions are perceived by means of various active and constraint forces. However at detailed consideration it often appears that these forces on essence are conditioned by interactions of atoms. If until recently practical necessity of detailed quantitative description of such interactions did not arise then in the modern world such knowledge are extremely called as finally just they would be a key to understanding, explanation, forecasting and programming of properties of substances. After opening by E. Rutherford in 1911 of the natural center of atom – nucleus the understanding has come that interaction between atoms results from overlapping of their electronic shells. In this connection has arisen necessity for calculation of overlapping integrals. Now at the decision of problems of physical chemistry and generally at quantum-mechanical description of properties of substances the concept of overlapping integral appears fundamental one. Let us write down the most general view two-center integral.

     (1)

where  – radiuses-vectors which are drawn from two before given centers 1 and 2 in any point A of space, dv – is the differentially-small volume located near to point A. Subintegral function  is defined by physics of the phenomenon described by corresponding overlapping. In a case, for example, of electrostatic interactions  is represented as product of charging density of the first atom and the potential created by the second atom. This potential, in turn, also can be found as a result of integration on space of charging density of the second atom. Great American physics J. C. Slater was the first who has faced to the problem of calculation of two-centered integrals. [1-5]. To present time so huge number of works are devoted to decision of this problem that even list of references to them would be occupy some hundred of pages. The most full review of works devoted to the given theme is presented in [6-8]. Many authors concentrate their attention at subintegral function and in dependence on it choose both system of coordinates and the scheme of integration. So C.W. David [9] for subintegral function which presented as product of two exponent offers use the Cartesian, spherical or elliptic coordinates. In according with made choice the expression for differentially-small volume is constructed. The author prefers the last variant as, in his opinion, just the elliptic coordinates are more acceptable for execution of numerical integration and subsequent approximation of overlapping integrals by algebraic functions. To the same opinion adhere Z. Romanovski, A.F. Jalbout [10]. Since 70-th years of last century to present time big contribution to development of art of two-centered integrals calculation is brought by I .I. Gusseinov [11-15], B.A. Mamedov. [14-16], M.P. Barnet [17-19]. Meanwhile the natural scheme of integration lies just on the surface. This scheme allows avoid any approximated methods and in some cases find analytical view of overlapping integrals.

Scheme of integration

Let R is the distance between centers 1 and 2. Position of any point A relatively these centers is unequivocally determined by distances r₁ and r₂ and corner φ of turn of plane 1А2 around of straight 1-2. So without of belittling subintegral function in (1) can be presented as dependent on four scalar arguments f(R, r₁, r₂, φ). Let us draw two series of spheres one of which is centered in point 1 and another – in point 2. Then in plane passed through these centers and point A the traces of these spheres form the pattern shown in figure 2. Let’s pick out pair of spheres in radiuses r₁ and r₁+dr₁ from the first series, pair of spheres in radiuses r₂ and r₂+dr₂ from the second series and pair of planes which passed through the centers 1 and 2 and oriented at corners φ and φ+dφ accordingly.

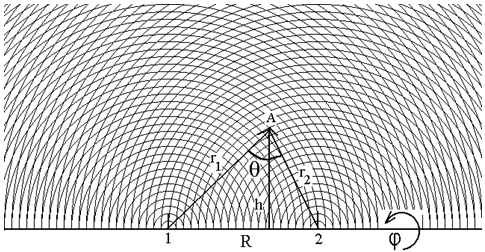
Figure 1 – Pattern formed by two series of co-centered spheres on plane which passed through centers 1 and 2

 

These three pairs of surfaces near integration point allocate a differentially-small parallelepiped which volume is equal

    (2)

where h dφ is its thickness, h – distance from point of integration to straight 1–2, ds – square of base section. This section ABCD is represented in figure 2 in the increased scale. The base square ds is equal to product of the basis on height . As , where θ – corner between vectors  , then

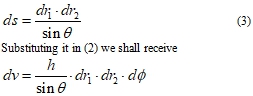     (4)

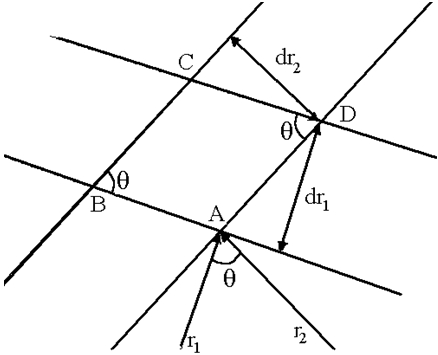
Figure 2 – Parallelogram – trace of crossing of two pairs of spheres

It is visible from consideration of figure 1 that the square of triangle 1A2 is equal

 

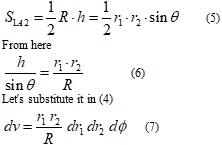
Now it is necessary correctly specify limits of integration. To each fixed corner φ correspond sets of half rings – traces of crossing of plane 1А2 by spheres of the first and second series (figure 1). For definiteness we shall reset half rings from the first series changing their radiuses from zero to infinity. Each such half ring is crossed by set of half rings of the second series. Thus r₂ changes from ׀r₁-R ׀ to ׀r₁+R׀. Thus the overlapping integral (1) gets the following general view:

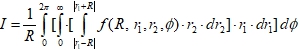        (8)

It appears often that overlapping of spherical-symmetrical functions centered in points 1 and 2 takes place. In this case dependence of subintegral function on R and φ disappears and integration on φ gives 2π. Then the expression (8) becomes simpler.

         (9)

Last expression is most acceptable to numerical integration. For its optimization it is necessary only choose an identical step of integration on variables r₁ and r₂ (Δr₁=Δr₂=Δr) as it takes place in figure 1 and to find value of overlapping integral only on distances multiple to a step.

At last absolutely simple expression arises when subintegral function represents product of two spherical-symmetrical functions one of which depends on r₁ and another – on r₂.

        (10)

In this case

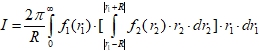       (11)

Often it success the integration on r₂ to execute analytically. Then for finding of overlapping integral it remains execute numerical integration only on one variable that essentially simplifies the procedure as whole. In some cases, especially at calculation of electrostatic interactions, it success completely avoid application of numerical methods and receive exact analytical view of overlapping integral.

Example

As the elementary example illustrated work of the offered scheme let us get expression for energy of coulombic interactions of point charge q₁ fixed in the center 1 with charge q₂ distributed under Gauss law centered in 2. That is, the electronic density of charge 2 is described by distribution

      (12)

On the one hand the required energy can be found as energy of point charge which is in potential of Gauss cloud. This potential on distance r from the center of the cloud is found by help of Ostrogradski-Gauss theorem.

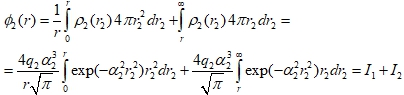       (13)

For simplification it was accepted in (13) that proportionality coefficient in Coulomb law is equal 1. The first integral in (13) is taken by parts and equal

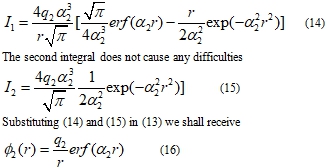
The required expression for coulombic energy is found as product of charge q₁ on potential φ₂ at value of its argument equal R

        (17)

On the other hand the potential of dot charge q₁ on distance r₁ from it is equal , and differentially-small charge of Gauss cloud on distance r₂ from its center is equal

        (18)

In terms of the considerable scheme

      (19)

Expression for the same energy can be found by substitution (19) in (11)

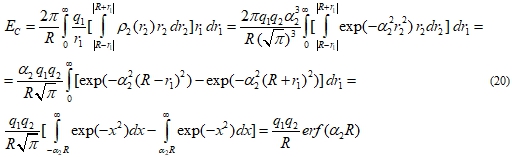
that completely coincides with (17). Thus legitimacy and efficiency of the offered scheme is proved.

Conclusion

I have worked out that scheme in 1981. Just it has allowed receive the exact analytical view of expressions for energy of interaction of atoms having arbitrary spherical-symmetric electronic shells [20]. In turn, on the basis of these expressions the numerical values of parameters of electronic shells for atoms of different chemical elements were determined [21]. The constructed by such manner interatomic potentials were successfully applied then to forecasting of mechanical properties of steels and alloys of a complex chemical composition [22]. However, during tens years I did not interest by publications on the given question, naively believing that the expounded manner of integration goes without of saying and used everywhere at necessity. I hope that the present publication allow reduce problems which as a matter of fact should not be.