ЛИНЕЙНЫЙ АНАЛИЗ МОДЕЛЕЙ МЕЛКОЙ ВОДЫ С УЧЕТОМ НЕОДНОРОДНОСТИ ДНА | Опубликовать статью РИНЦ

Шантыр А.Л.

Магистрант, Волгоградский государственный университет

ЛИНЕЙНЫЙ АНАЛИЗ МОДЕЛЕЙ МЕЛКОЙ ВОДЫ С УЧЕТОМ НЕОДНОРОДНОСТИ ДНА

Аннотация

В статье приведены результаты линейного анализа динамики малых возмущений в моделях мелкой воды. Решены краевые задачи Штурма-Лиувилля для уравнений Сен-Венана и модифицированной модели в приближении Буссинеска в случае неровного дна. Обсуждаются особенности  зависимостей собственной частоты от волнового числа.

Ключевые слова: модель мелкой воды, уравнение Буссинеска, линейный анализ, дисперсия волн.

Shantyr A.L.

Master, student Department of information systems and computer modeling, Volgograd State University

THE LINEAR ANALYSIS OF MODELS OF SMALL WATER TAKING INTO ACCOUNT HETEROGENEITY OF THE BOTTOM

Abstract

The results of the linear analysis of the dynamics of small perturbations in the shallow water models are discussed. Boundary problems of Storm Liouville for Saint-Venant’s equations and the modified model in approach of Boussinesq in case of a rough bottom are solved. Features of dependences of own frequency from wave number are disputed.

Keywords: model of small water, Boussinesq equation, linear analysis, the wave dispersion.

Введение. Актуальность данной работы заключается в определении области применимости моделей мелкой воды [2]. Выявляются пределы зависимости собственной частоты от волнового числа для каждой системы уравнений. Формулируется и решается краевая задача Штурма-Лиувилля.

Целью работы является моделирование динамики поверхностных вод на случай неровного дна (появление дисперсионных эффектов).

Модели поверхностных вод в случае неровного дна. Уравнения «мелкой» воды являются уравнениями гиперболического типа и описывают течение несжимаемой жидкости на твердой поверхности. Данная модель получается из полной системы уравнений Навье–Стокса [2]. Без учёта сил Кориолиса и придонного трения в одномерном случае для неоднородного дна  имеем [6]:

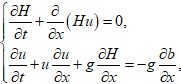      (1)

где  b(x) ­­– функция дна, u(x) – компонента скорости. Модифицированная модель Сен-Венана в приближении Буссинеска будет выглядеть следующим образом:

     (2)

где β – параметр дисперсии;  – скорость распространения волны. Обе эти модели описывают динамику с учетом дисперсионных эффектов [5].

Краевая задача Штурма-Лиувилля. Поставим краевую задачу для систем (1) и (2). Для этого необходимо линеаризовать системы. Рассмотрим данный процесс относительно малых возмущений:

    (3)

Возмущенные величины представляются в виде:

Линеаризованные уравнения для модели Сен-Венана (1) с учетом (3) примут вид:

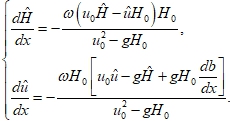     (4)

В рамках ВКБ-приближения линейная система уравнений (4)  позволяет получить выражения на собственные значения (собственные частоты) и собственные функции:

 

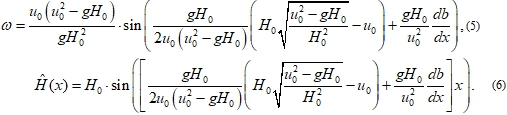
Зависимость собственной частоты от волнового числа представлена на рисунке 1.

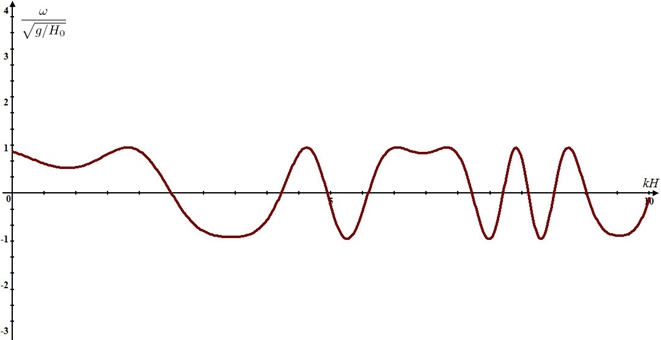
Рис. 1 – Дисперсионная зависимость частоты волны от волнового числа

Для численного решения использовался метод стрельбы. Программная реализация краевой задачи Штурма-Лиувилля представлена на рисунке 2.

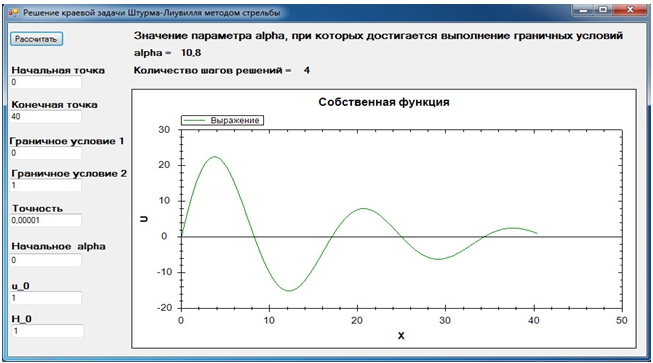
Рис. 2 – Решение краевой задачи Штурма-Лиувилля

 

Линеаризованное уравнение для модифицированной модели в приближении Буссинеска (2) с учетом (3) можно записать в виде:

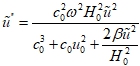   (7)

Используя уравнение Бернулли, получаем следующий набор собственных значений (частот) и собственных функций:

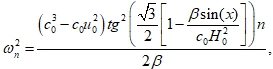        (8)

        (9)

Набор собственных частот и собственная функция для данного вида системы уравнений представлена на рисунках 3, 4. Характерной особенностью является нелинейная зависимость.

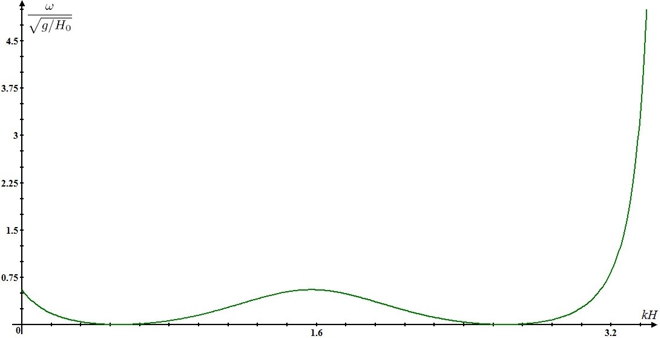
Рис. 3 – Зависимость собственной частоты от волнового числа (модифицированное приближение Буссинеска)

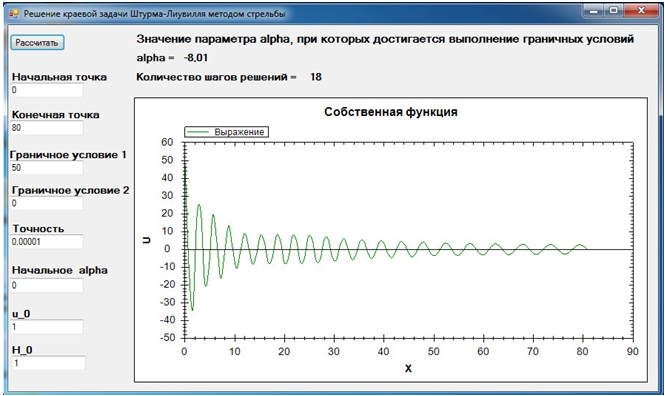
Рис. 4 – Решение краевой задачи Штурма-Лиувилля (модифицированное приближение Буссинеска)

Из рисунка 3 можно сделать вывод о том, что модифицированная модель мелкой воды в приближении Буссинеска применима при kh~3,2. Собственная функция представляет собой затухающую со временем волну. Варьируя граничные условия, будем получать различные наборы собственных частот и функций. При увеличении числа точек разбиения имеем сходимость численного решения.

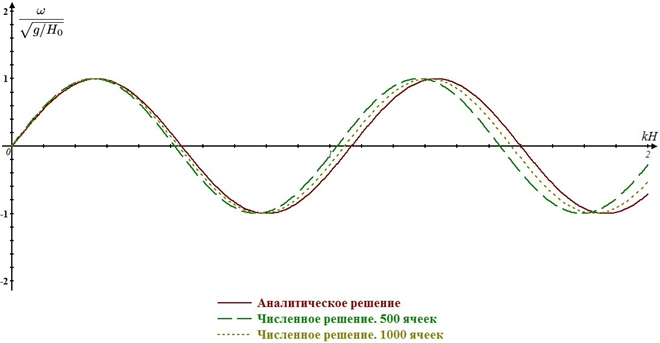
Рис. 5 – Сходимость численного решения

Заключение. Рассмотренная в работе неоднородность в моделях «мелкой» воды эквивалентна появлению дисперсии (групповая скорость волнового пакета отлична от скорости распространения каждой волны по отдельности) [5]. Оценки  параметра дисперсии в модели мелкой воды, например, для реки со средней глубиной 5 метров дают значения порядка 20 .

Работа выполнена при поддержке гранта РФФИ 13-01-97062.