ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА-ДУГЛАСА НА ЭКОНОМИКЕ ХОРЕЗМСКОЙ ОБЛАСТИ РЕСПУБЛИКИ УЗБЕКИСТАН | Опубликовать статью ВАК, elibrary (НЭБ)

Абдуллаев И.С.

Кандидат экономических наук, доцент, Ургенчский государственный университет

ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА-ДУГЛАСА НА ЭКОНОМИКЕ ХОРЕЗМСКОЙ ОБЛАСТИ РЕСПУБЛИКИ УЗБЕКИСТАН

Аннотация

В статье рассматривается одна из важных проблем моделирования экономической динамики – выбор наилучшей производственной функции, описывающей производственные процессы протекающие в хозяйственных системах.

Ключевые слова: производственная функция, моделирование, экономическая динамика.

Abdullaev I.S.

PhD in Economics

Associate professor, Urgench state university

COBB-DOUGLAS PRODUCTION FUNCTION IN THE ECONOMY OF KHOREZM REGION OF UZBEKISTAN

Abstract

In the article considered one of the main problems of modeling dynamics of economy – choice of best production function, describing production processes running in economic systems.

Keywords: production function, modeling, dynamics of economy.

Для моделирования работы производственной системы используют зависимость результатов производства от используемых ресурсов, не изучая в деталях сам процесс преобразования ресурсов в производственный результат.

По сути, предлагается рассматривать производство как «черный ящик», на вход которого поступают ресурсы x₁,x_2,x₃, …, x_n, а на выходе получается некоторый результат y₁,y₂,y₃, … y_m:

Y = f ( X ) .                                                                           (1)

Если рассматривать только один какой-то производственный результат при нескольких ресурсах, то зависимость становится многофакторной:

(2)

 

Модель (2) называют «производственной функцией».

Если попытаться в максимальной степени приблизить модель производственной функции к экономическим реалиям, то необходимо включить в неё все используемые ресурсы, но такая модель становится очень не удобной для анализа и при вычислении её коэффициентов приходится сталкиваться со значительными сложностями, основной из которых является неустойчивость оценок этих коэффициентов. Поэтому и в теории, и на практике останавливаются на основных ресурсах – труд L и капитал K. Логика выделения этих двух типов ресурсов такова: есть живой труд, который применяется каждым работающим на предприятии непосредственно, и есть результаты труда – это станки, механизмы, сырьё и т.п. – всё это, как легко убедиться, было создано трудом других людей и даже – других поколений, то есть – овеществлённый труд.

Чаще всего под капитальными ресурсами понимают величину основных фондов, а под трудовыми ресурсами – количество занятых в производстве.

Из всего многообразия возможных моделей производственных функций выбирают и используют степенные функции, а среди этих моделей применяют производственную функцию Кобба-Дугласа, которая, с учётом ранее введённых обозначений, имеет вид:

 (3)

где A — коэффициент нейтрального технического прогресса; α – показатель степени, причём его значения лежат в пределах от нуля до единицы:

0 < α < 1.                                                                         (4)

Определим свойства этой модели.

Прежде всего, необходимо указать на то, что в случае, когда хотя бы один ресурс будет равен нулю, производственный результат также будет равен нулю, что следует признать соответствующим реальной экономике:

0,L)=F(K,0)=0,                                                                     (5)

Следующее свойство этой функции заключается в том, что при неограниченном увеличении одного из ресурсов выпуск также неограниченно растет, то есть:

                                                              (6)

Вычислим теперь первые производные (3) по каждому ресурсу. Получим:

 

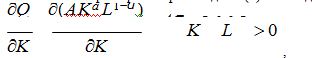                        (7)

 

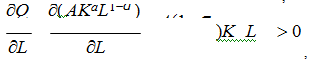    (8)

 

так как показатель степени, в соответствии с начальными условиями (4) положителен и меньше единицы. Выявленное свойство имеет простой экономический смысл, а именно положительность первых производных означает, что с ростом любого из ресурсов выпуск растет, а с его уменьшением – снижается.

Насколько эти два свойства модели соответствует экономической реальности?

Свойство (6), свидетельствующее о том, что с ростом любого из ресурсов выпуск растет, выполняется только на определённом интервале изменения ресурсов. Пусть, например, фиксированы капитальные ресурсы, то есть здания, сооружения и, самое существенное, станки и технологические линии являются неизменными. С ростом трудовых ресурсов будет наблюдаться рост производства, но до тех пор, пока загрузка оборудования не станет 100%. Дальнейшее увеличение трудового ресурса потребует работу в две смены, а для работающих во вторую смену, как известно, устанавливаются стимулирующие надбавки, то есть отдача

 

трудового ресурса уменьшается. Ещё большее увеличение трудового ресурса приведёт к тому, что работать придётся в три смены, и хотя объём производимой продукции возрастает, отдача трудового ресурса ещё больше уменьшается, и как следствие этого увеличивается себестоимость производства. Когда рабочие работают в три смены и оборудование загружено круглосуточно, дальнейшее увеличение трудового ресурса не приведёт к увеличению объемов, а наоборот – рабочие будут мешать друг другу, поскольку на одном рабочем месте будет работать несколько человек. А это означает, что объёмы производства даже будут уменьшаться! Следовательно, условие (6) не выполнимо на практике.

Аналогичный вывод можно сделать и по отношению к капитальному ресурсу. Вычислим теперь вторые производные функции Кобба-Дугласа по факторам:

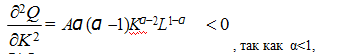     (9)

 

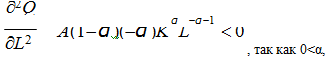   (10)

 

Итак для функции Кобба-Дугласа характерна положительная первая производная (7) и (8) и отрицательная вторая производная по ресурсам (9) и (10). Для какого типа экономики выполняются эти два условия одновременно? Для ответа на этот вопрос рассмотрим изменение ресурсоотдачи. Напомним, что под ресурсоотдачей в экономической теории понимается приращение производственного результата на единицу прироста ресурса. Ресурсоотдача, как известно, с ростом ресурса сначала возрастает, затем становится постоянной, а затем – убывает. На каждом из этих трёх этапов меняются как первая, так и вторая производная по ресурсу. На первом этапе возрастающей отдачи, когда производство ещё далеко от номинальных значений, первая и вторая производная положительны. На втором этапе, этапе постоянной отдачи ресурса, первая производная положительна и является величиной постоянной, а вот вторая производная при этом равна нулю. При убывающей отдаче ресурса, на третьем этапе, первая производная хотя и положительна, но убывает, а вторая производная – отрицательна. А из этого можно сделать вывод о том, что условия (7) – (8) и (9) – (10), которые являются свойствами функции Кобба-Дугласа, отражают последний этап ресурсоотдачи, то есть – неэффективное производство, когда привлекаемые ресурсы дают меньший результат, чем в условиях постоянной или возрастающей ресурсоотдачи.

Итак, из проведённого анализа следует, что производственная функция Кобба-Дугласа может хорошо описывать производственный процесс, если он находится в стадии перегрузки как производственных мощностей, так и трудовых ресурсов, когда объёмы производства превышают номинальные значения и само производство в результате этого неэффективно.

Покажем, как это отражается в реальной экономике на примере Хорезмской области республики Узбекистан. В табл. 1 приведены статистические данные по области за период с 1998 по 2012 год.

Таблица. 1. Статистические данные по экономике Хорезмской области

Год	Валовой региональный продукт, млн. сум	Основные фонды, млр. сум	Численность занятых, тыс. чел.
1998	152,20	624,4	449,00
1999	144,30	640,7	456,00
2000	148,60	671,7	467,20
2001	283,50	713,8	468,30
2002	372,80	755,7	478,30
2003	483,20	799,9	490,40
2004	562,00	930,4	506,60
2005	930,20	1010,9	522,30
2006	1 003,70	1091,1	538,00
2007	1 236,10	1230,5	547,00
2008	1375,30	882,9	588,2
2009	1 547,80	997,8	606,7
2010	1 944,10	1010,8	637,5
2011	2306,70	1290,9	639,2
2012	2945,80	1366,5	643,4

Источник: Статистический ежегодник Узбекистана-2012.

Для того чтобы построить модель экономической динамики, эти данные были приведены к безразмерным величинам. Функция Кобба-Дугласа (3), параметры которой найдены с помощью метода наименьших квадратов, имеет вид:                                                                (11)

Но так как по определению показатель степени не может быть меньше нуля или быть больше единицы, то убеждаемся в том, что эта функция бессмысленна и не может использоваться для анализа реальной экономики.

Поэтому следует признать, что производственная функция Кобба-Дугласа имеет ограниченный диапазон применения и не является универсальной.