ПЕРЦЕПТИВНЫЕ ИНТЕГРАЛЬНЫЕ ПАТТЕРНЫ –СПОСОБ БЫСТРОГО ТРЕКИНГА ЗРАЧКА НА ОСНОВЕ ОТКЛИКА ANN-MLP ПЕРСЕПТРОНА И МОДИФИЦИРОВАННОГО ЧИСЛЕННОГО МЕТОДА ДИФФЕРЕНЦИАЛЬНОЙ ЭВОЛЮЦИИ | Опубликовать статью ВАК, elibrary (НЭБ)

DOI: https://doi.org/10.23670/IRJ.2022.120.6.001

ПЕРЦЕПТИВНЫЕ ИНТЕГРАЛЬНЫЕ ПАТТЕРНЫ –СПОСОБ БЫСТРОГО ТРЕКИНГА ЗРАЧКА
НА ОСНОВЕ ОТКЛИКА ANN–MLP ПЕРСЕПТРОНА И МОДИФИЦИРОВАННОГО
ЧИСЛЕННОГО МЕТОДА ДИФФЕРЕНЦИАЛЬНОЙ ЭВОЛЮЦИИ

Научная статья

Грушко Ю.В.^*

ORCID: 0000-0002-3663-0018,

Камчатский государственный университет им. Витуса Беринга, Петропавловск-Камчатский, Россия

^* Корреспондирующий автор (neuralpill[at]gmail.com)

Аннотация

В статье предлагается быстрая и точная модель регистрации и трекинга зрачка глаза «RAPID-AN» в задаче видеоокулографии для устройств с ограниченным вычислительным ресурсом (слабые персональные компьютеры, встраиваемые системы на базе архитектуры ARM) с целью снижения стоимости технологии для индивидуального использования людьми с ограниченными возможностями здоровья и медицинскими учреждениями.В основу модели легла идея представления процесса регистрации зрачкав кадре (поиск координат центра и размера региона, наиболее полно аппроксимирующего зрачок) как задачи глобальной многомерной оптимизации.Целевая функцияформализована как значение отклика ANN-MLPперсептрона над интегральными паттернами, в яркостном смысле схожими со структурой искомого объекта (зрачок-радужка) – концепция перцептивных интегральных паттернов. С целью улучшения сходимости к экстремумупредложена модификация метода дифференциальной эволюции, в основе которой лежит процесс формирования генетических изоляций популяции решений в окрестностях всех локальных и глобальных экстремумов целевой функции, с последующим ростом наиболее приспособленной изоляции (рядом с глобальным экстремумом) и вырождением иных, в соответствии с дифференциальным уравнением Ферхюльста-Пирла. Данное поведение делает метод поиска менее «жадным» и дает возможность корректно выделять зрачок из полного кадра.

Модель решает задачу регистрации зрачка с ошибкой не более 1 – 2% на тестовых датасетахи высокой скоростью ~ 8,35 мс. в режиме трекинга на архитектуре BCM2837 ARMCortex-A53 1200 МГц (встраиваемые системы).

Проведен сравнительный анализ и показана эффективность модели в сравнении с некоторыми существующими детекторами: сверточные нейронные сети архитектурыTinyYolov3, метод Виолы-Джонса (Хаар-Каскады) и др.

Ключевые слова: видеоокулография, нейронная сеть, дифференциальная эволюция, детектор.

PERCEPTUAL INTEGRAL PATTERNS AS A METHOD FOR RAPID PUPIL TRACKING
BASED ON ANN-MLP PERCEPTRON RESPONSE AND A MODIFIED NUMERICAL METHOD
OF DIFFERENTIAL EVOLUTION

Research article

Grushko Yu.V.^*

ORCID: 0000-0002-3663-0018,

Kamchatka State University, Petropavlovsk-Kamchatsky, Russia

^* Corresponding author (neuralpill[at]gmail.com)

Abstract

The article offers a fast and accurate model of registration and tracking  of pupils «RAPID-AN» in the task of video-oculography for devices with a limited computing resource (weak personal computers, embedded systems based on ARM architecture), to reduce the technology cost for individual use by disabled people and by health facilities. The model was based on the idea of the pupil registration process in the frame (finding the center coordinates and the region size most fully capturing the pupil) as a global, multifaceted optimization task. The target function is formalized as the meaning of ANN-MLP response perceptron over integral patterns, in a vivid sense similar to the desired object structure (pupil-iris) – the concept of perceptual integral patterns. In order to improve the convergence to extremum, a modification of differential evolution method is proposed, based on the process of forming the genetic isolation of solutions population in the vicinity of all local and global extremes of the target function, with subsequent growth of the most adapted insulation (next to the global extremum) and the degeneration of others, according to the Verhulst-Pierre differential equation. This behavior makes the search method less «greedy» and makes it possible to correctly extract a pupil from the full frame.

The model solves the problem of pupils registration with an error of not more than 1 – 2% on test datasets and a high speed of ~ 8.35 ms. in tracking mode on the architecture of BCM2837 ARM Cortex-A53 1200 MHz (embedded systems).

The comparative analysis was conducted, and performance of the model in comparison with some existing detectors was shown: Tiny Yolo v3, Viola-Jones (Haar-Cascade) method, etc.

Keywords: video-oculography, neural net, differential evolution, detector.

Введение

Видеоокулография (ВОГ, айтрекинг) – это неинвазивная технология отслеживания положения глаз, имеющая широкое теоретическое и практическое значение: включая медицинские исследования в офтальмологии, мониторинге фотореакции в нейрореанимации посредством пупиллометрии [1], экспресс диагностике наркотической, алкогольной и промышленной интоксикации [2], в нашлемных системах индикации военно-воздушных сил, а также в биометрических системах идентификации по радужке (где первым этапом является поиск зрачка в кадре).

Наиболее актуальной задачей является разработка доступных аппаратно-программных комплексов альтернативной аугментативной коммуникации (АПК ААК) с использованием ВОГ для медицинских учреждений, реабилитационных центров, людей с болезнями двигательного нейрона и другими заболеваниями центральной нервной системы (ЦНС), такими как латеральный амиотрофический склероз (БАС) МКБ-10 G12, диплегия G 80.1, спинальная мышечная атрофия G12.1, синдром запертого человека G83 и другие.

У пациентов с вышеперечисленными синдромами наблюдается полная потеря речи (афазия), паралич бульбарной и мимической мускулатуры, тетраплегия (потеря функций конечностей), при полной сохранности сознания. При этом остается возможность коммуникации с пациентами с помощью движения глаз.

Так на момент 2016 года было завершено проведение крупного исследования журналом Lancet, показывающего, что только больных с БАС на 2016 г. насчитывается ~ 330 918 человек, а также намечен прирост заболеваемости на 100 000 населения на 4 – 5% за последние 26 лет [3]. Распространенность диплегии в России приходится в среднем от 1.5 – 4 на 1000 новорожденных [4], не говоря про другие заболевания ЦНС, что делает разработку методов трекинга и доступных систем ААК, с использованием ВОГ, актуальной задачей.

Этап регистрации и трекинга зрачка в существующих алгоритмах занимает значительное время и вычислительные ресурсы, требует высокопроизводительного специализированного оборудования (например, Tobii Dynavox), что делает данную технологию недоступной для большинства медицинских учреждений и индивидуального использования пациентами.

Так существующие методы, используемые в ВОГ, можно разбить на несколько классов.

Методы, основанные на пороговой сегментации и математической морфологии, имеют невысокую точность, но вычислительно просты и в своей основе опираются на тот факт, что при использовании инфракрасной (ИК) подсветки, расположенной параллельно оптической оси видеоокулографа, зрачок в кадре становится самой темной областью в кадре (используется в пупиллометрах Neuroptics DP-2000, NPi). Проводится бинаризация кадра. Как результат образуется наибольшее связное множество точек, яркости которых ниже порога [5]. Лишние объекты, оставшиеся после сегментации: ресницы, темные области на роговице удаляются операторами эрозии (только в том случае, если сгущения ресниц не сливаются со зрачком в одну связную компоненту, и они меньше зрачка), а оставшаяся область зрачка наращивается морфологической дилатацией с тем же количеством итераций и ядром. В случае попадания бликов на границу зрачка вычисляются минимальные выпуклые оболочки (например, методом Джарвиса), после находится центр масс контура [6]. В [7] используется адаптивная бинаризация на основе исследования процентильной функции. Не менее интересные техники основаны на применении рекурсивной эрозии [8] и морфологической обобщенной функции расстояния. Данные подходы не учитывают особенность функционирования зрительного аппарата – процессы миоза и мидриаза зрачка при ИК-подсветке глаза, что существенно уменьшает их точность.

Методы на основе исследования гранично-ступенчатой модели изображения: преобразования Хафа и модификации [9], RANSAC, Starburst [10], ElSe [11], Swirski [12]. Интуитивный адаптивный метод на основе исследования энтропии градиентов краевых сегментов [13]. Класс обладает хорошей точностью, так преобразование Хафа устойчиво к утере части границы зрачка. Поиск происходит в трехмерном пространстве – центр и радиус зрачка или множество его граничных точек. Недостаток данного класса – большая вычислительная сложность. Методу на основе построения оптимального кругового пути [8] необходимо знать начальную точку, которая должна находиться внутри области интереса зрачка.

Методы, основанные на пространственной свертке и корреляции [12], [14] имеют большую вычислительную сложность, не устойчивы к паразитному освещению, но обладают свойством поиска по определенному паттерну или части изображения. Такие методы в большинстве случаев не нуждаются в использовании ИК-подсветки глаза, что является преимуществом без использования дополнительного оборудования.Наиболее быстрой моделью можно назватьалгоритм Виолы-Джонса [15], основанный на свертках с признаками Хаара (над интегральным представлением изображения), значение которых поступают в каскадный классификатор для принятия решения относительно нахождения объекта.

Применяя сверточные (Yolo) [6] или генеративно-состязательные нейронные сети (U-net, Seg-net) в задаче ВОГ [16] можно добиться высокой точности, учитывая индивидуальные особенности строения зрительного аппарата пациента (например, в случае колобомы радужной оболочки). У сверточных моделей есть большой недостаток – они вычислительно сложны по причине наличия большого числа сверточных фильтров, выделяющих признаки на гранично-ступенчатой модели изображения. Так для достижения 30 FPS для передовой TinyYolo, необходимы ресурсы карты GPUPascalTitanX. Также большинство моделей имеют достаточно сложный жизненный цикл обучения, что потребует работы профильного специалиста в области машинного обучения, увеличивая затраты на использование ВОГ.

В данной работе делается попытка учесть достоинства и недостатки вышеперечисленных методов. Решается задача быстрого и точного выделения зрачка глаза в кадре в условиях ограниченных вычислительных ресурсов (слабые ПК, смартфоны, встраиваемые системы на базе архитектуры ARM) с целью снижения стоимости технологии для индивидуального использования людьми с ОВЗ, медицинскими учреждениями и реабилитационными центрами.

В основу модели легла идея представления процесса регистрации зрачка в кадре – поиск координат центра и размера региона, наиболее полно аппроксимирующего зрачок, как задачи глобальной многомерной оптимизации и ее решение метаэвристическим численным методом дифференциальной эволюции.

Для повышения точности детектирования в качестве целевой функции предлагается использовать значение отклика многослойного персептрона (ANN-MLP сеть) над интегральными паттернами, в яркостном смысле схожими со структурой искомого объекта (структура зрачок-радужка).

Формализация задачи регистрации зрачка

Будем считать регионом интереса зрачка (ROI) сегментированную область кадра, представляющуюзрачок с окружающей его радужной оболочкой.

Правильно найденный ROI зрачка позволит:

1) снизить вычислительные затраты алгоритмов ВОГ–вычислительная сложность уменьшится пропорционально отношению размера кадра к размеру региона;

2) правильно определить величину порога для адаптивной сегментации зрачка (выделения точек зрачка из ROI), «исключая» диапазоны яркости, не принадлежащие зрачку (отсутствует необходимость в анализе гистограммы всего кадра);

3) исключить «шумовые» граничные точки областей, не относящихся к зрачку, что актуально в случае дальнейшего применения методов исследующих гранично-ступенчатую модель изображения;

4)успешно использовать алгоритмы, для которых необходимо или желательно (Starburst, AIPF, [17]) знать начальную точку, принадлежащую компоненте зрачка.

5) радикально ускорить преобразование Хафа за счет уменьшения радиуса области поиска при найденных параметрах ROI.

Так как здоровый зрачок представляет из себя компактную область эллиптической/круглой формы и содержит пиксели, интенсивности которых ниже, чем окружающая его радужная оболочка, а приблизительное соотношение размера зрачка к радужной оболочке составляет 1/3 (средний размер радужки 12 мм., зрачка – 3.25-5 мм.), единовременно учесть все параметры поможет поиск по паттерну.

При разработке алгоритма приходилось учитывать физиологические особенности зрительного аппарата человека: реактивность, миоз – сжатие зрачка (не более 1.1 мм.), как реакция на свет и мидриаз – его расширение (до 8 мм.).

Пусть дан трехканальный кадр F(u), а R,G,B  – красный, зеленый и синий каналы соответственно (двумерные матрицы), тогда воспользуемся взвешенным методом  для перевода F(u) в градации серого f(u).

Чтобы определить параметры региона интереса зрачка   – точка в двумерном пространстве на изображении) располагающегося f(u) в  размером , предлагается дескриптор, однозначно выделяющий точки центра зрачка и его размера из точек изображения.

Перцептивный интегральный паттерн – дескриптор, состоящий из окна поиска  w описываемого точкой  , разделенного на k сегментовтаким образом, чтобы наиболее полно аппроксимировать структуру искомого объекта в яркостном смысле,иANN-MLP нейросети (многослойный персептрон), принимающей на вход нормализованный вектор значений интенсивностей сегментов окна w.  сеть осуществляет задачу бинарной классификации т.е. нейрон выхода возвращаетстепень уверенности в диапазоне , где1 – соответствует наилучшемуположению и размеру (точки экстремума ) паттерна над зрачком (или другим искомым объектом).

Вектор интенсивностей сегментовпаттернаможно вычислить, используя интегральную матрицу 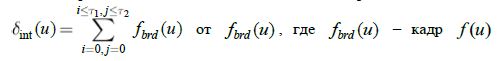 от , где  – кадр  с реплицированными паддингами размера  , где  – максимально допустимый размер поиска объекта. Репликация используется для корректного расчета значения паттерна на краях кадра. Одной из особенностей интегральной матрицы является возможность очень быстро вычислять значение суммарнойинтенсивностипроизвольного сегмента паттерна минимум за 3 операции.

Пустьимеется паттерн в точке , который разбит на k=9 сегментов, расположенных в виде сетки. Тогда вычисление вектора интенсивностей  можно описать Алгоритмом 1.

В случае использования паттернов с более сложной структурой (не в форме сетки), применение вложенных циклов будет невозможно, в этом случае необходимо воспользоваться формулой, представленной в 7-й строке алгоритма, для расчета интенсивностей каждого сегмента отдельно.

Сформировав вектор, передадим его на входной слой MLP сети, которая определит, есть ли над паттерном зрачок.

Алгоритм 1 – Вычисление вектора интенсивностей

вектор интенсивностей сегментов паттерна в точке (нормализация убирает взаимосвязь между размером окна паттерна и значениями интенсивностей)  –многослойный персептрон.

В таблице 1 представлена структура сети, для задачи (1).

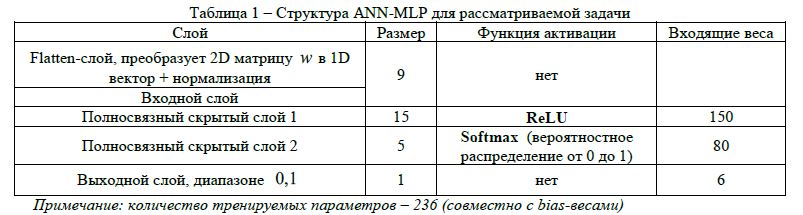
Увеличение размеров первого скрытого слоя уменьшило влияние сигналов входа друг на друга, а также увеличило количество тренируемых весовых коэффициентов, что положительно сказалось на точности работы сети.

Модель разработана и обучена в библиотеке Keras на языке Python 3.10, и затем переведена на С++17 в формат.model (использовался keras2cpp модуль [18]) для использования в режиме реального времени.

В лаборатории КамГУ им. Витуса Беринга были разработаны обучающие и тестовые выборки из видеорядов: изображения глаз в инфракрасном диапазоне (IR) и в видимом диапазоне (NIR). Сами выборки представлены в виде текстовых файлов с наборами векторов вида  – вероятность принадлежности вектора зрачку (0 или 1).

В качестве видеоокулографов, для создания выборок, использовались: Web-камера (0.3 МП, 30 Гц), с удаленным ИК-фильтром, и двумяSMD ИК-диодами (ближнего спектра ~940 нм. подключенные параллельно через резисторы номиналом 120 Ом к VCC и GND каналам камеры) для регистрации методом темного зрачка; камера смартфона 8 МП – регистрация зрачка в видимом спектре.

На рисунке 1 продемонстрированы графики обучениянейросети для (1).

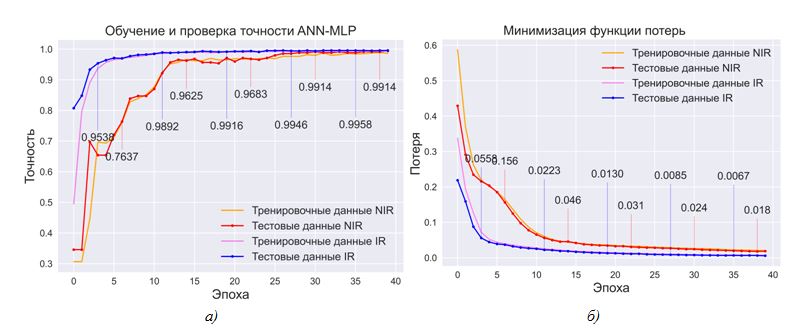
Рис. 1 – Процесс обучения ANN-MLP для поиска зрачка с помощью перцептивных интегральных паттернов:

(а) график точности распознавания на тренировочных и тестовых наборах данных; (б) ошибка распознавания

Для итеративного обновления весов сети на обучающих данных был использован алгоритм Adam показавший высокую эффективность [19]в задачах глубокого обучения. При обучении сети выполняется минимизация функции потерь, в качестве которой выступила бинарная кросс-энтропия:

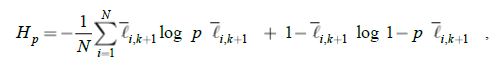
где – крайний элемент i-го вектора выборки, означающий реальную вероятность (1 – паттерн, описываемый вектором точно над зрачком, 0 – в противном случае), p– прогнозируемая вероятность, –размер выборки. На каждую эпоху, в процессе обучения, используется по 15 векторовиз тренировочной части выборки (размер батча).Как видно, в процессе обучения средняя ошибка снижается (ось «Потеря»), в то время как точность распознавания (ось «Точность») доходит до ~99.5%.

Кривые точности тестовых датасетовхорошо аппроксимируют кривые тренировочных (не уходя вниз), показывая отсутствие переобучения сети – ситуаций, когда построенная модель хорошо прогнозирует примеры из обучающей выборки, но не работает на примерах из тестовых выборок.

Для выбора методики решения поставленной задачи, необходимо произвести полный расчет целевой функции (просчитать куб, по всем трем измерениям) на изображениях глаз, взятых из баз CASIA-IrisV4 [20] Института автоматизации Китайской академии наук и LPW [21].Анализ (1)представлен втаблице2.

Примеры проекций целевых функций (в точке максимума) по оси  представлены на рисунке 2 (изображения созданы в Matplotlib и Python 3.10).

Сравнительный анализ метаэвристик в задаче регистрации зрачка

Для решения (1) воспользуемся метаэвристическими численными методами глобальной оптимизации. Были изученыи протестированы: дифференциальная эволюция (ДЭ) [22], [23], метод имитации отжига (МИО) [24], [25], [26], генетические алгоритмы (ГА) [27],[28], метод роя частиц (МРЧ) [29]. Рассмотрены работы [30],[31], а также проведен сравнительный анализ к исходной задаче, в результате чего выбран наиболее оптимальный– метод ДЭ.

Дифференциальная эволюция – метод стохастической многомерной глобальной оптимизации, моделирующий процессы мутации, кроссовера и селекции особей в популяции.

Рис. 2 – Примеры проекций целевых функций:

(а) кадр из видеопотока базы LPW; (б) проекция целевой функции в максимуме =118, генерируемая сетью на 15 эпохе обучения (~96% точности); (в) на 40 эпохе (~99%); (г, е) тестовые изображения из базы ORL;
(д, ж) проекции функции в =11

В процессе исследования ДЭ удалось выявить основные преимущества, благодаря которым метод можно использовать в (1): быстродействие; робастность; надежность в исследовании нелинейных, мультимодальных функций, без знания пространства поиска (функция зависит от изображения);

Пусть требуется решить (1), исходная популяция решений состоит из n индивидов,  , а пространство поиска 3-х мерное. Тогда популяция t-го поколения описывается множеством  где – возможное решение, характеризующееся набором генов .

ДЭ на каждой итерации включает три процесса: мутацию, кроссинговер и селекцию наилучшей особи.

В мутации для каждого целевого   . С помощью целевого и двух случайных векторов образуется новый вектор мутации .

Для применения в практических целях метод должен находить решение с вероятностью близкой к единице (для построения корректных пупиллограмм, управлении ПК взглядом и др.). В случае с ДЭ вероятность сходимости к глобальному максимуму возрастает при увеличении n. С другой стороны, увеличение популяции замедляет скорость сходимости, а соответственно нахождения региона, чего нельзя допустить на устройствах со слабым вычислительным ресурсом (смартфоны, микропроцессорные архитектуры).

Чтобы получить высокую вероятность нахождения глобального решения на мультимодальной функции, сохраняя приемлемую сходимость, предлагаются новые модели мутации, кроссинговера и селекции. Обозначим предложенную модификацию, как стратегию поиска наиболее приспособленной генетической изоляции (Strategy for Finding the most Adapted Genetic Isolation – SFAGi) и формально зададим ее как систему, используя дифференциальное уравнение модели ограниченного роста популяций – Ферхюльста-Пирла [32]:

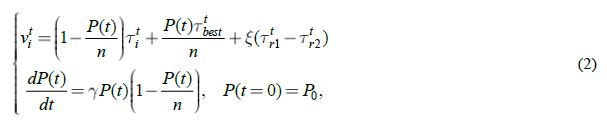
где  P – размер изоляции в момент времени t, P_o – начальный размер изоляции. Аналитическое решение дифференциального уравнения из системы (1) находится путем разделения переменных и интегрирования:

Тогда окончательный вид модели мутации, используемый в программном комплексе видеоокулографии, учитывая (2) и (3), записывается как:

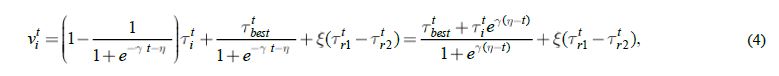
где  – специально включенный коэффициент,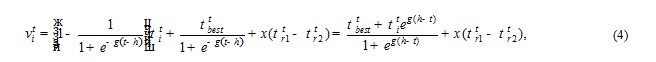 задающий время эволюции изоляций (задержка по осиOX),   – удельная скорость роста наилучшей генетической изоляции (Мальтузианский параметр),  – лучшее найденное положение всей популяцией за t итераций,  – сила мутации, амплитуда возмущений, вносимых в генофонд.

В предлагаемой модели, в силу ее стохастической природы, размер наилучшей изоляции задается в виде коэффициента передачи в диапазоне , где 1 – максимально достигнутая емкость изоляции равная n, а 0 – полное отсутствие особей в изоляции (или очень малое количество особей, попавших в окрестность максимума во время начального распределения).

Первый этап (4) – исследовательский поиск, отвечает за появление генетических изоляций в зависимости от ландшафта функции, т.е. изоляции формируются вокруг всех экстремумов, как локальных, так и глобальных (рисунок 5). С течением , каждая из изоляций динамически моделирует особенности рельефа функции (так называемого ландшафта приспособленности), подстраивая под них распределение «внутреннего» источника энтропии , в процессе чего находится наилучшее решение по каждой из изоляции, что исключает «жадность» алгоритма и схождение к локальным решениям.

Второй этап (4) отвечает за динамику роста  наиболее приспособленной генетической изоляции. Изоляция, имеющая наибольшее значение целевой функции, с течением времени начинает расти, тогда как другие, менее приспособленные – вырождаются. Увеличение популяции решений в наиболее приспособленной изоляции дает более детальный поискв окрестности , а следовательно, и более точную сходимость, в отличие от классической интерпретации ДЭ, что актуально в условиях малого размера начальной популяции.

Модель мутации ведет себя нелинейно (рисунок 3а, б, рисунок 4).

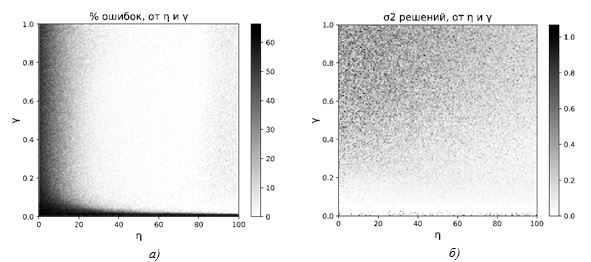
Рис. 3 – Зависимость точности решений модифицированной модели мутации от входных параметров:

(а) процент ошибок; (б) разброс решений-кандидатов относительно максимума

В процессе экспериментов было замечено, что увеличение времени эволюции изоляций  гарантирует наиболее точное нахождение области, в которой присутствует глобальный максимум, а уменьшение удельной скорости роста  , дает наиболее точное приближение к  , т.е. минимальную дисперсию решений относительно максимума.

По окончании операции мутации, выполним оператор кроссинговера над целевым и мутантным вектором, в результате получим пробный вектор , где каждый компонент определяется как:

В связи с тем, что отклик MLP нелинеен и принимает различные значения и положения глобального экстремума (зрачка в кадре может не быть или он может быть частично скрыт), предложенная схема показывает лучшие результаты в процессе детектирования, в сравнении с фиксированным количеством итераций или достижением определенного значения оптимума.

Условие останова напрямую коррелирует с параметрами  и  – метод гарантированно сойдется за конечное время используя (7).

После достижения условия останова получаем ненормализованные координаты (с учетом паддингов)  региона интереса зрачка – центр и размер, и нормализованные координаты (в системе координат кадра) 

Был проведен сравнительный анализ следующих метаэвристических методов(рисунок 4):

1. Дифференциальная эволюция SFAGi. Используемые параметры: .
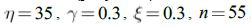2. Метод имитации отжига. Использовался сверхбыстрый отжиг Л.Ингбера [26] для работы в режиме реального времени (отжиг Больцмана [24] и Коши [25] имеют лучшую точность, но не пригодны из-за медленной сходимости); Параметры: начальная температура .
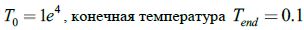3. Генетический алгоритм вещественного кодирования с оператором инбридинга [27] для концентрации поиска в локальных узлах и BLX-кроссинговером [27]. Для отбора особей в новую популяцию использовался эллитизм [28] т.е. отбор 30% наиболее приспособленных особей из получившихся потомков и их родителей в новую популяцию, оставшиеся 70% индивидов генерируются случайно, используя равномерный закон распределения. В результате данной техники метод преодолевает локальные экстремумы, не допускает потерю лучших решений и быстро сходится; Параметры: n=55, эллитизм e=30%.
4. Метод роя частиц [29].Параметры: весовая доля инерции 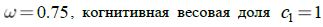, социальная весовая доля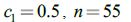 

В таблице 2 представлен расчет дисперсии – меры разбросарешений относительно глобального экстремума. Расчеты показывают, как точно метод находит центр зрачка (колебания детектора по осям абсцисс и ординат) и размер региона интереса (точность аппроксимации зрачка регионом).

Так как методы относятся к классу стохастических, было произведено по 1000 программных пусков для каждого метода. Правильное решение – точка, в окрестности 

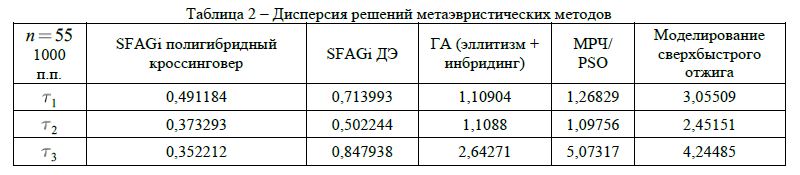
Сравнительный анализ показывает, что модифицированныйДЭSFAGi сходится на порядок быстрее других метаэвристик, позволяет использовать сравнительно невысокие значения размеров исходной популяции (минимальное n=21, что влияет на общую скорость поиска ROI зрачка), и находить точное значение экстремума в нелинейных мультимодальных функциях, даже в том случае, когда множество допустимых решений функции очень мало.

В процессе тестирования у ГА была замечена требовательность к вычислительным ресурсам – большая часть времени уходит на сортировку индивидов в процессе элитарного отбора и инбридинга.

Особенности модели «RAPID-AN» в режиме трекинга объекта

Описанные выше шаги можно использовать для обработки кадров /медицинских изображений – назовем это режимом детектирования.

В режиме трекинга модель «RAPID-AN» значительно ускоряется без потери точности. Для этого используются некоторые приемы, описанные ниже.

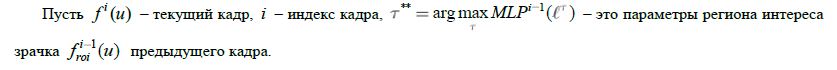
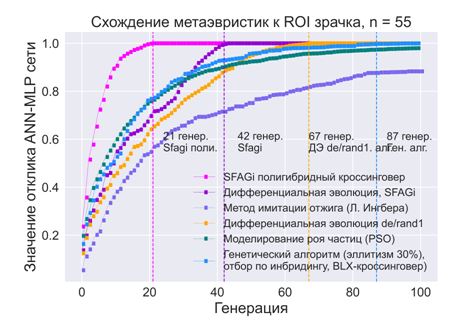
Рис. 4а – Сравнительный анализ метаэвристических методов в задаче (1): усредненные графики схождения к глобальному экстремуму (1000 пусков)

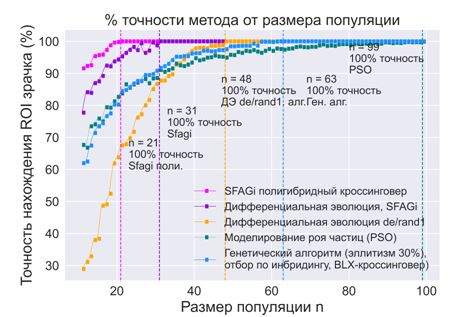
Рис. 4б – Сравнительный анализ метаэвристических методов в задаче (1): % точности найденного ROI
от размера популяции метода

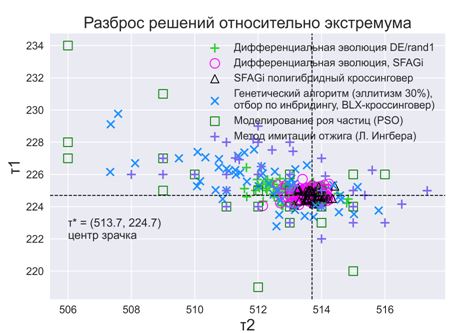
Рис. 4в – Сравнительный анализ метаэвристических методов в задаче (1): разброс решений
относительно экстремума

1. Вычисление реплицированных паддингов и интегральной 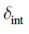матрицы проводится не для всего кадра, а для 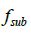– безопасный регион поиска, который определяется точкой экстремума предыдущего кадра как 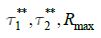и его пересечением (оверлеем)  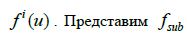в виде отдельного кадра, в котором отсутствует вся ненужная информация (белый прямоугольник на рисунке 6в). Таким образом мы ищем параметры зрачка не в кадре размером , а в матрице с максимально возможным размером , содержащую только зрачок (без потери качества объекта, в отличии от создания пирамиды изображений).
2. Размер паддингов 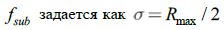 (данный вариант более устойчив к изменениям среднего уровня освещенности кадра и изменению размеров зрачка) или же корректируется в зависимости от размера ROI, найденного на предыдущем кадре, т.е.  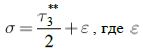где – коэффициент компенсирующий увеличение размеров зрачка.
3. Начальная популяция генерируется внутри 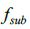. Проекции ограничены областью  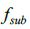по каждой координате. Такое поведение позволяет игнорировать локальные экстремумы, расположенные далеко от центра зрачка, увеличивая точность (фактически, область 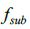содержит только зрачок), в результате чего размер начальной популяции можно сократить до 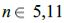. В качестве сверхбыстрого генератора псевдослучайных чисел используется Xorshift128 (G. Marsaglia), генератор сдвигового регистра 128-битной версии.
4. Поскольку поиск происходит в 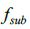, уменьшается время исследования функции до 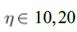и увеличивается Мальтузианский параметр до 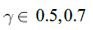, что автоматически уменьшает количество итераций сходимости алгоритма до 30 – 32, без потери точности.

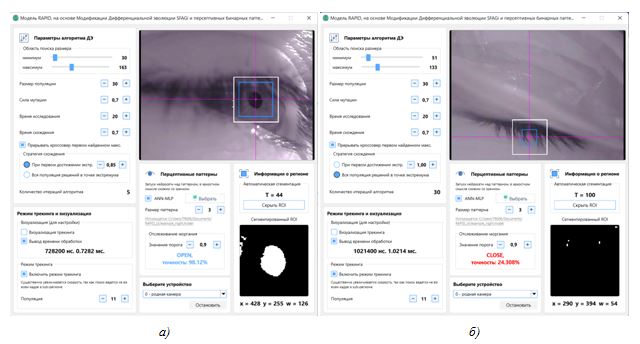
Рис. 5 – Пример работы модели«RAPID-AN»

Разработанный детектор регистрации и трекинга зрачка

Общая схема работы детектора на основе перцептивных интегральных паттернов и модификации численного метода ДЭ представлена на рисунке 6.

Детектор разработан в виде ООП библиотеки RAPID_AN.h/cpp на языке программирования С++17 и выложен под GNUGeneralPublicLicensev3.0 [33] на GitHub.

Данная библиотека может использоваться для разработки программных комплексов аугментативной коммуникации для коммуникации людей с нервнопаралитическими синдромами, а также при разработке новых алгоритмов ВОГ в качестве первого быстрого этапа поиска ROI с последующим уточнением координат зрачка и размера в нем.

Предоставляемый основной функционал библиотеки: 1) метод класса std::vectorRAPID::detect(cv::Mat&) –поиск региона интереса зрачка методом SFAGi иперсептивными паттернами. Возвращаемый вектор  нормализован относительно системы координат кадра. В качестве параметра выступает ссылка на трехканальный кадр . 2) Геттер cv::Mat&RAPID::getROIMat(void) – возвращает ссылку на , матрица может быть использована для дальнейшей обработки компоненты зрачка методами Хафа, RANSAC, математической морфологии, контурного анализа. 3) Геттер uint8_t RAPID::getAdaptedThresh(void) – возвращает адаптивный порог в диапазоне , рассчитанный на основе параметров региона, наиболее полно аппроксимирующего зрачок и корректно выделяющий его из фона.

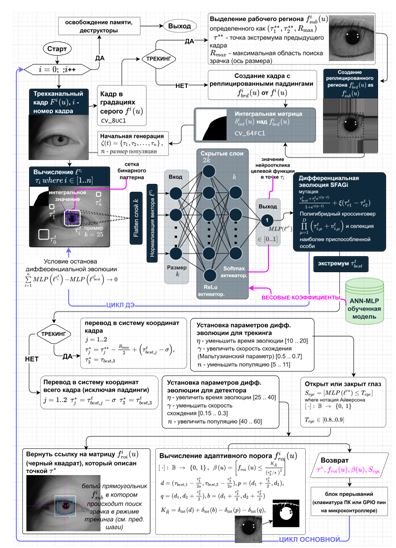
Рис. 6 – Общая схема модели регистрации и трекинга зрачка «RAPID-AN»

4) int8_t RAPID::getEyeState(float) – в случае, если поиск зрачка осуществляется посредством перцептивных интегральных паттернов, метод вернет 1 – если глаз открыт (т.е. если точность предсказания ANN-MLP сети больше некоторого порога), 0 – если закрыт, в противном случае -1. 5) float RAPID::getANNConfidence(void) –отклик сети в точке  в процентах. 6) long long int RAPID::getNumIteration(void) – получение номера итерации схождения алгоритма.

На рисунке 7 представлено окно программного комплекса, разработанного с использованием RAPID_AN.h иQt 6.0, демонстрирующее работу детектора. Имеется возможность установки параметров движка ДЭ, загрузки обученной модели, просмотра положения и размеров найденного ROI, просмотра времени обработки и результата адаптивной пороговой сегментации, состояния открытия глаза, точности распознавания и др.

Рис.7 – Программный комплекс трекинга зрачка:

(а) состояние открытого зрачка, сегментированный регион, размер региона и координаты зрачка;

(б) состояние закрытого зрачка

На рисунке 6 представлен разработанный визуально-ориентированный конструктор ANN-MLP для задачи (1), с возможностью просмотра структуры сети, загрузки и редактирования обучающей выборки и параметров обучения, а также обучения самой модели (с наглядными графиками). Комплекс разработан на Python 3.10, PySide 2, Keras, TensorFlow и OpenCV 4.5.3.

Сравнительный анализ

Бенчмарк работы предложенной модели на различных архитектурах представлен в таблице 3.

Для замера времени использовалась библиотека и метод std::chrono::steady_clock::now(). Для преобразования полученного результата в наносекунды std::chrono::duration_cast().

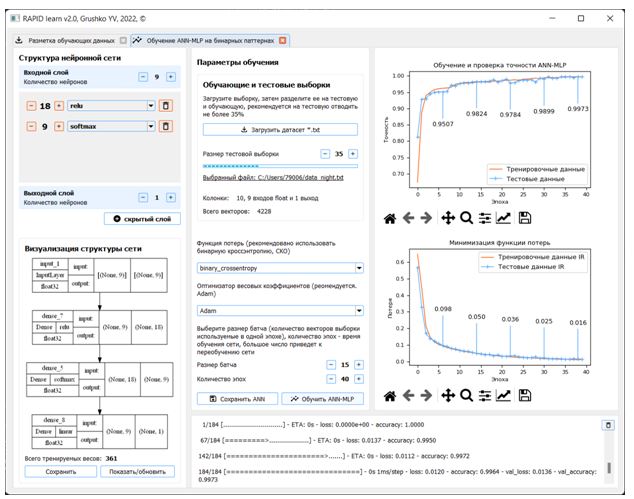
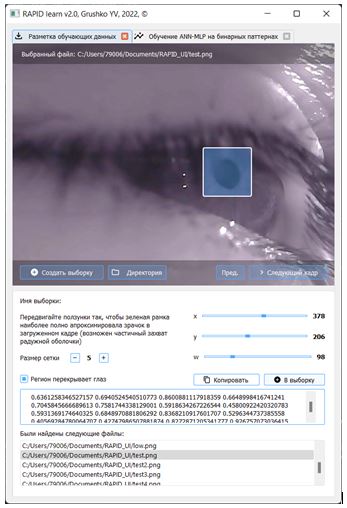
Рис.8 – Визуально-ориентированный конструктор нейросетевых моделей
и их обучения«RAPID-AN learn» для задачи (1)

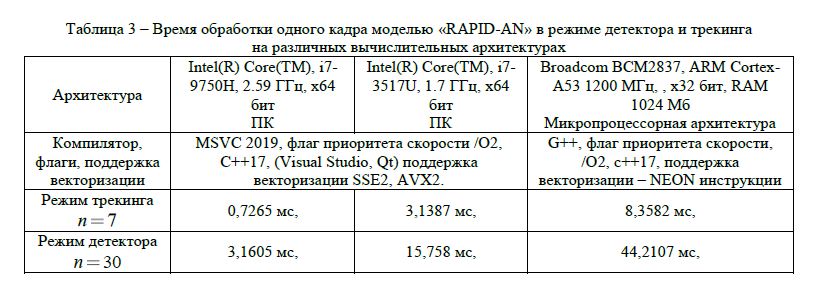
В таблице 4 приводятся результаты анализа детекторов, основанных на часто используемых техниках поиска объекта на изображении.

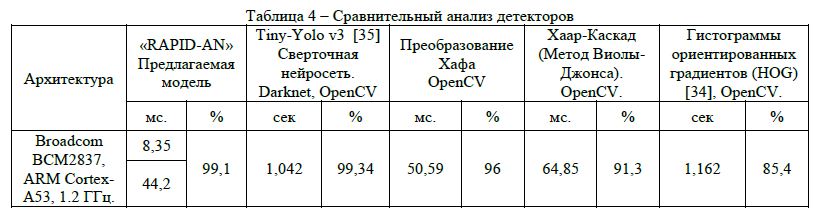
Предложенная модель позволяет подойти к процессу регистрации зрачка пошагово, сначала находится регион, наиболее полно аппроксимирующий зрачок, тем самымудаляются«лишние» объекты, мешающие точному поиску, затем локально, применяется один из методов, основанный на изучении граничной модели изображения, контурного анализа или математической морфологии.

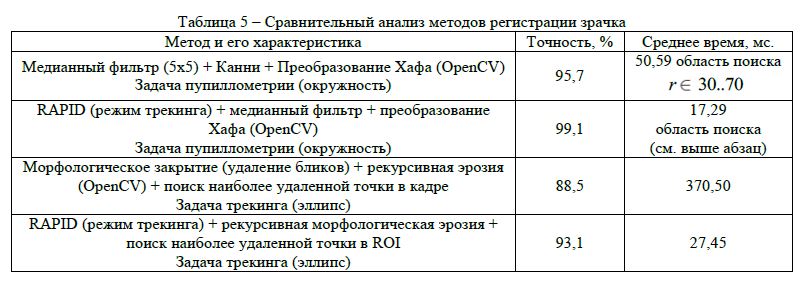
Пример использования модели с различными методиками представлен в таблице 5.

Найденный  и его параметры  позволяют значительно уменьшить время и область поиска радиуса зрачка (например, при преобразовании Хафа [9] или рекурсивной морфологической эрозии [8]), а также исключить большинство ложных окружностей. Таким образом область поиска составит  .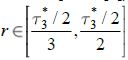

Заключение

Предлагаемая модель регистрации и трекинга зрачка глаза «RAPID-AN», основанная на поиске региона, наиболее полно аппроксимирующего зрачок, модифицированным численным методом ДЭSFAGi и перцептивными интегральными паттернами, была успешно применена в задаче ВОГ с целью снижения вычислительных затрат, что дает возможность применять алгоритмы на неспециализированных устройствах (ПК, оснащенных веб-камерой) и микропроцессорных архитектурах (очки айтрекеры), а также удешевить технологию ВОГ, сделав ее более доступной для людей с ОВЗ и медицинских учреждений.

Сравнительный анализ детекторов показал существенное снижение вычислительных затрат в рассматриваемой задаче, и высокую точность благодаря использованной модификации ДЭ.

Поскольку метод дифференциальной эволюции, используемый в модели«RAPID-AN», относится к классу стохастических, необходимо было уменьшить процент ложных решений в результате спуска к локальным оптимумам и увеличить вероятность точного решения до единицы. В результате был предложен модифицированный численный метод ДЭ основанный на модели ограниченного роста Ферхюльста-Пирла. Кроссинговери операторы отбора были пересмотрены, что сделало модель более детерминированной ипозволило гарантированно двигаться в направлении наилучшего значения на каждой итерации.Определено условие остановаметода с учетом особенностей целевой функции.Модификация превзошла существующие методы в рассматриваемой задаче.

Разработанная модель в дальнейшем будет внедрена в АПК ААК на основе технологии ВОГ, описанного в смежной работе [6], а также проведено тестирование комплекса в реабилитационных центрах для лежачих больных после инсульта.

Дополнительно проведен эксперимент по регистрации сложных объектов в режиме реального времени. В теории, увеличив размерность сетки перцептивного паттерна можно аппроксимировать в яркостном смысле любой объект (по аналогии с методом прямоугольников).На рисунке 7 представлен результат эксперимента. Обработка одного кадра заняла 75.34 мс. на BCM2837, ARM Cortex-A53 и 6.15 мс. на Intel Core, i7-9750H.

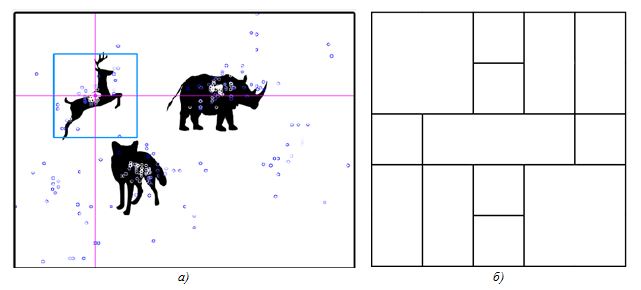
Рис. 7 –Результат эксперимента:

(а)поиск силуэта оленя сложным паттерном;(б) ( k=13, двухслойный ANN-MLP:
[вход 13]-[25]-[10]-[1 выход], n=30, 50 итераций)

Такой вычислительно простой детектор может применятся и в робототехнике, например, для беспилотного транспорта при распознавании дорожных знаков и разметкит.е. там, где применение сверточных нейронных сетей невозможно или нецелесообразно.

Тема детектирования объектов различных классов с помощью перцептивных паттернов и ДЭ будет раскрыта в дальнейших работах.

Благодарности Выражаю благодарность научному руководителю, доктору физико-математических наук Паровику Р. И. за замечания, способствовавшие выполнению работы.	Acknowledgement I express my gratitude to the supervisor, Doctor of Physical and Mathematical Sciences R.I. Parovik for a number of comments that contributed to the improvement of the presented work.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Списоклитературы / References

1. Oshorov A. Pupillometry as a method for monitoring of pupillary light reflex in ICU patients / A.Oshorov, Alexandrova, K.R.Muradyan et al. // Issues of N.N. Burdenko Neurosurgery. – 2021. – Vol. 85. – P. 117. DOI:10.17116/neiro202185031117.
2. КуцалоА. Л. Пупилометриявкачествеметодаэкспресс-диагностикинаркотическойинтоксикации: автореф. дис. канд. мед. наук: 14.00.20: защищена 2004 / Куцало Анатолий Леонидович. – СПб., 2004. – 18 с.
3. Logroscino Giancarlo. Global, regional, and national burden of motor neuron diseases 1990–2016: a systematic analysis for the Global Burden of Disease Study 2016 / Piccininni Marco, Marin Benoıt, Nichols Emma and others // The Lancet Neurology. – 2018. – Vol. 17. – P. 1083–1097.
4. Ткаченко Е. С. Детский церебральный паралич: состояние изученности проблемы / Е. С.Ткаченко, О. П.Голева, Д. В.Щербакови др.// МиД. – 2019. – №2. – С. 4-9.
5. Durna Y. Design of a Binocular Pupil and Gaze Point Detection System Utilizing High Definition Images / Y.Durna, F. Ari // Applied Sciences. – 2017. – Vol. 7. – P. 498.
6. Грушко Ю.В. Аппаратно-программный комплекс аугментативной системы коммуникации на основе технологии Eyetracking / Ю.В. Грушко // Вестник КРАУНЦ. Физ.-мат. науки. – 2019. – Т. 27. – №2.  – С. 55–73.
7. Bonteanu P. Robust Pupil Detection Algorithm Based on a New Adaptive Thresholding Procedure / P.Bonteanu, Cracan, G.Bonteanu et al. // IEEE International Conference on e-Health andBioengineering EHB. – 2019. – P. 276.
8. Матвеев И. А. Методы и алгоритмы автоматической обработки изображений радужной оболочки глаза.: дис. … докт. тех. наук : 05.13.11: защищена 30.10.2014 г. / Матвеев Иван Алексеевич. – М., 2014 – 290 с.
9. Alkuzaay M. Towards Accurate Pupil Detection Based on Morphology and Hough Transform / M.Alkuzaay, Alshemmary // Baghdad Science Journal. – 2020. – Vol. 17. – N. 2. – P. 583–590.
10. Dongheng L. A hybrid algorithm for video-based eye tracking combining feature-based and model-based approaches / L.Dongheng, D.Winfield, D. J. Parkhurst // IEEE Computer SocietyConference on Computer Vision and Pattern Recognition. – – Vol. 3. – P. 79.
11. Fuhl W. ElSe: ellipse selection for robust pupil detection in real-world environments / W.Fuhl, T.Santini, T. Kubler et al. // The Ninth Biennial ACM Symposium. – 2016. – P. 123–130.
12. L. Robust real-time pupil tracking in highly off-axis images / Bulling. A. Dodgson. N. // Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA). – 2012. – P. 173–176.
13. Topal Cihan. An Adaptive Algorithm for Precise Pupil Boundary Detection using Entropy of Contour Gradients / Topal Cihan, CAKIR Halil, Akinlar Cuneyt. – 2017.
14. Yang Z. Intelligent Evaluation of Strabismus in Videos Based on an Automated Cover Test / Z. Yang // Applied Sciences. – 2019. – P. 59.
15. Paul Viola. Rapid Object Detection using a Boosted Cascade of Simple Features / Paul Viola. // Conference on computer vision and pattern recognition. –
16. Fuhl W. The Applicability of CycleGANs for Pupil and Eyelid Segmentation / Fuhl Wolfgang, Geisler David, Rosenstiel Wolfgang, Kasneci Enkelejda. // Data Generation and Image Refinement. – 2019. – P. 4406–4415.
17. Grushko Y. V. Fast Pupil Tracking based on the Study of a Boundary-stepped Image Model and Multidimensional Optimization Hook-Jives Method / Y. V.Grushko, R. I. Parovik // Informatics and automation. – 2021. – Vol. 2. – 435–462.
18. Перевозчиков Г. Keras2cpp [Электронный ресурс] / Г. Перевозчиков // GitHub. – 2019.– URL: https://github.com/gosha20777/keras2cpp (дата обращения 04.22)
19. Kingma D. A. A Method for Stochastic Optimization / Kingma Diederik, Ba Jimmy // International Conference on Learning Representations. – 2014.
20. Chinese Academy of Sciences Institute of Automation. Iris image database, ver. 4. – 2021. – [Electronic resource] URL: http://www.cbsr.ia.ac.cn/china/Iris20Databases20CH.asp.
21. Tonsen Marc. Labeled pupils in the wild: A dataset for studying pupil detection in unconstrained environments / Zhang Xucong, Sugano Yusuke, Bulling Andreas // ACM International Symposium on Eye Tracking Research and Applications (ETRA) – 2016. – P. 139-142 doi:10.1145/2857491.2857520
22. Jeyakumar G. Convergence Analysis of Differential Evolution Variants on Unconstrained Global Optimization Functions / Jeyakumar Gurusamy, C. Shanmugavelayutham // International Journal of Artificial Intelligenceand Applications. –
23. Meera R. FSDE-Forced Strategy Differential Evolution used for data clustering / Meera Ramadas, Ajith Abraham, Sushil Kumar // Journal of King Saud University – Computer and Information Sciences. – – Vol. 31, –N. 1. – P. 52–61.
24. Kirkpatrick S. Optimization by Simulated Annealing / S.Kirkpatrick, C. D.Gelatt Jr., M. P. Vecchi // Science. – – Vol. 220. – P. 671-680.
25. Szu H. H. Fast Simulated Annealing / H. H.Szu, R. L. Hartley // Physical Letters. – – Vol. 122. – P. 157-162.
26. Ingber L. Very fast simulated re-annealing / L. Ingber // Mathematical and Computer Modelling. – – Vol. 12. – P. 967-973.
27. Cervantes A. An empirical comparison of two crossover operators in real-coded genetic algorithms for constrained numerical optimization problems. / Cervantes Adriana, Mezura-Montes Efrén, Coello Carlos. // IEEE International Autumn Meeting on Power, Electronics and Computing, ROPEC. – doi:10.1109/ROPEC.2014.7036347.
28. Панченко, Т. В. Генетические алгоритмы: учебно-методическое пособие / Т. В. Панченко, под ред. Ю. Ю. Тарасевича. –Астрахань : Издательский дом «Астраханский университет», 2007. – 87 [3] с.
29. Poli R. Particle Swarm Optimization: An Overview. / Kennedy James, Blackwell Tim // Swarm Intelligence. –
30. Ковалевич А. А. Исследование стохастических алгоритмов оптимизации для применения в имитационном моделировании систем / А. А.Ковалевич, А. И.Якимов, Д. М.Албкеират // Информационные технологии. – – № 8. – С. 55-60.
31. Пупков К. А. Алгоритм «Дифференциальной эволюции» для задачи технического проектирования / К. А.Пупков, В. А.Феоктистов // Информационныетехнологии. – – № 8. – С. 25-31.
32. Tsoularis A. N. Analysis of Logistic Growth Models / A. N.Tsoularis, Wallace James // Mathematical biosciences. – – Vol. 179. – P. 21–55.
33. Грушко Ю. В. RAPID [Электронный ресурс] / Грушко Ю. В. // GitHub. – 2022. – URL: https://github.com/NeuralPill/RAPID (дата обращения 21.04.22).
34. Dalal N. Histograms of oriented gradients for human detection / N. Dalal, B. Triggs // IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR). – – P. 886-893. DOI: 10.1109/CVPR.2005.177.
35. Adarsh P. YOLO v3-Tiny: Object Detection and Recognition using one stage improved model / Adarsh Pranav, Rathi Pratibha, Kumar Manoj. – 2020.– 687-694. DOI:10.1109/ICACCS48705.2020.9074315.

Список литературы на английском языке / References in English

1. Oshorov A. Pupillometry as a method for monitoring of pupillary light reflex in ICU patients / A.Oshorov, Alexandrova, K.R.Muradyan et al. // Issues of N.N. Burdenko Neurosurgery. – 2021. – Vol. 85. – P. 117. DOI:10.17116/neiro202185031117.
2. Kucalo A. L. Pupilometrija v kachestve metoda jekspress-diagnostiki narkoticheskoj intoksikacii [Pupilometry as a method of rapid diagnosis of drug intoxication]: abstract dis. … of PhD in Medicine: 14.00.20: defense of the thesis 2004 / Kucalo Anatolij Leonidovich. – SPb., 2004. – 18 p. [in Russian]
3. Logroscino Giancarlo. Global, regional, and national burden of motor neuron diseases 1990–2016: a systematic analysis for the Global Burden of Disease Study 2016 / Piccininni Marco, Marin Benoıt, Nichols Emma and others // The Lancet Neurology. – 2018. – Vol. 17. – P. 1083–1097.
4. Tkachenko E. S. Detskij cerebral’nyj paralich: sostojanie izuchennosti problemy [Cerebral Palsy: State of Research on the Problem] / E. S.Tkachenko, O. P.Goleva, D. V.Shherbakov et al. // MiD [Mother and Child in Kuzbass]. – 2019. – №2. – P. 4-9. [in Russian]
5. Durna Y. Design of a Binocular Pupil and Gaze Point Detection System Utilizing High Definition Images / Y.Durna, F. Ari // Applied Sciences. – 2017. – Vol. 7. – P. 498.
6. Grushko Y.V. Apparatno-programmnyj kompleks augmentativnoj sistemy kommunikacii na osnove tehnologii Eyetracking [Hardware-software complex of augmentative communication system based on eyetracking technology] / V. Grushko // Vestnik KRAUNC [Bulletin KRAUNZ]. – 2019. – V. 27. – №2.  – P. 55–73. [in Russian]
7. Bonteanu P. Robust Pupil Detection Algorithm Based on a New Adaptive Thresholding Procedure / P.Bonteanu, Cracan, G.Bonteanu et al. // IEEE International Conference on e-Health andBioengineering EHB. – 2019. – P. 276.
8. Matveev I. A. Metody i algoritmy avtomaticheskoj obrabotki izobrazhenij raduzhnoj obolochki glaza [Methods and algorithms for automatic processing of iris images]: dis. … of Dr. in Physics and Mathematics: 05.13.11: defense of the thesis 30.10.2014 г. / Matveev Ivan Alekseevich. – M., 2014 – 290 p. [in Russian]
9. Alkuzaay M. Towards Accurate Pupil Detection Based on Morphology and Hough Transform / M.Alkuzaay, Alshemmary // Baghdad Science Journal. – 2020. – Vol. 17. – N. 2. – P. 583–590.
10. Dongheng L. A hybrid algorithm for video-based eye tracking combining feature-based and model-based approaches / L.Dongheng, D.Winfield, D. J. Parkhurst // IEEE Computer SocietyConference on Computer Vision and Pattern Recognition. – – Vol. 3. – P. 79.
11. Fuhl W. ElSe: ellipse selection for robust pupil detection in real-world environments / W.Fuhl, T.Santini, T. Kubler et al. // The Ninth Biennial ACM Symposium. – 2016. – P. 123–130.
12. L. Robust real-time pupil tracking in highly off-axis images / Bulling. A. Dodgson. N. // Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA). – 2012. – P. 173–176.
13. Topal Cihan. An Adaptive Algorithm for Precise Pupil Boundary Detection using Entropy of Contour Gradients / Topal Cihan, CAKIR Halil, Akinlar Cuneyt. – 2017.
14. Yang Z. Intelligent Evaluation of Strabismus in Videos Based on an Automated Cover Test / Z. Yang // Applied Sciences. – 2019. – P. 59.
15. Paul Viola. Rapid Object Detection using a Boosted Cascade of Simple Features / Paul Viola. // Conference on computer vision and pattern recognition. –
16. Fuhl W. The Applicability of CycleGANs for Pupil and Eyelid Segmentation / Fuhl Wolfgang, Geisler David, Rosenstiel Wolfgang, Kasneci Enkelejda. // Data Generation and Image Refinement. – 2019. – P. 4406–4415.
17. Grushko Y. V. Fast Pupil Tracking based on the Study of a Boundary-stepped Image Model and Multidimensional Optimization Hook-Jives Method / Y. V.Grushko, R. I. Parovik // Informatics and automation. – 2021. – Vol. 2. – 435–462.
18. Perevozchikov G. Keras2cpp [Keras2cpp] [Electronic resource] / Perevozchikov G. // GitHub. – 2019.– URL: https://github.com/gosha20777/keras2cpp (accessed: 21.04.2022). [in Russian]
19. Kingma D. A. A Method for Stochastic Optimization / Kingma Diederik, Ba Jimmy // International Conference on Learning Representations. – 2014.
20. Chinese Academy of Sciences Institute of Automation. Iris image database, ver. 4. – 2021. – [Electronic resource] URL: http://www.cbsr.ia.ac.cn/china/Iris20Databases20CH.asp.
21. Tonsen Marc. Labeled pupils in the wild: A dataset for studying pupil detection in unconstrained environments / Zhang Xucong, Sugano Yusuke, Bulling Andreas // ACM International Symposium on Eye Tracking Research and Applications (ETRA) – 2016. – P. 139-142 doi:10.1145/2857491.2857520
22. Jeyakumar G. Convergence Analysis of Differential Evolution Variants on Unconstrained Global Optimization Functions / Jeyakumar Gurusamy, C. Shanmugavelayutham // International Journal of Artificial Intelligenceand Applications. –
23. Meera R. FSDE-Forced Strategy Differential Evolution used for data clustering / Meera Ramadas, Ajith Abraham, Sushil Kumar // Journal of King Saud University – Computer and Information Sciences. – – Vol. 31, – N. 1. – P. 52–61.
24. Kirkpatrick S. Optimization by Simulated Annealing / S.Kirkpatrick, C. D.Gelatt Jr., M. P. Vecchi // Science. – – Vol. 220. – P. 671-680.
25. Szu H. H. Fast Simulated Annealing / H. H.Szu, R. L. Hartley // Physical Letters. – – Vol. 122. – P. 157-162.
26. Ingber L. Very fast simulated re-annealing / L. Ingber // Mathematical and Computer Modelling. – – Vol. 12. – P. 967-973.
27. Cervantes A. An empirical comparison of two crossover operators in real-coded genetic algorithms for constrained numerical optimization problems. / Cervantes Adriana, Mezura-Montes Efrén, Coello Carlos. // IEEE International Autumn Meeting on Power, Electronics and Computing, ROPEC. – doi:10.1109/ROPEC.2014.7036347.
28. Panchenko, T. V. Geneticheskie algoritmy: uchebno-metodicheskoe posobie [Genetic algorithms: tutorial] / Panchenko, T. V. Edited by Ju. Ju. Tarasevicha. – Astrahan’ : Publishing house «Astrahanskij universitet». 2007. – 87 [3] p.
29. Poli R. Particle Swarm Optimization: An Overview. / Kennedy James, Blackwell Tim // Swarm Intelligence. –
30. Kovalevich, A. A. Issledovanie stohasticheskih algoritmov optimizacii dlja primenenija v imitacionnom modelirovanii sistem [Study of stochastic optimization algorithms for use in simulation of systems] / A. A.Kovalevich, I.Jakimov, D. M. Albkeirat // Informacionnye tehnologii [Information technologies]. – 2011. – № 8. – P. 55-60. [in Russian]
31. Pupkov K. A. Algoritm «Differencial’noj jevoljucii» dlja zadachi tehnicheskogo proektirovanija [Algorithm «Differential evolution» for the problem of technical design] / K. A.Pupkov, V. A. Feoktistov // Informacionnye tehnologii [Information technologies]. – 2004. – № 8. – P. 25-31. [in Russian]
32. Tsoularis A. N. Analysis of Logistic Growth Models / A. N.Tsoularis, Wallace James // Mathematical biosciences. – – Vol. 179. – P. 21–55.
33. Grushko Y. V. RAPID [RAPID] [Electronic resource] / Grushko Y. V. // GitHub. – 2022. – URL: https://github.com/NeuralPill/RAPID. (accessed: 21.04.2022). [in Russian]
34. Dalal N. Histograms of oriented gradients for human detection / N. Dalal, B. Triggs // IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR). – – P. 886-893. DOI: 10.1109/CVPR.2005.177.
35. Adarsh P. YOLO v3-Tiny: Object Detection and Recognition using one stage improved model / Adarsh Pranav, Rathi Pratibha, Kumar Manoj. – 2020.– 687-694. DOI:10.1109/ICACCS48705.2020.9074315.