К ВОПРОСУ СОЗДАНИЯ ЦИФРОВОЙ ОБРАЗОВАТЕЛЬНОЙ СРЕДЫ ДЛЯ ОБУЧЕНИЯ МАТЕМАТИКЕ В ПРОЦЕССЕ ПОДГОТОВКИ СПЕЦИАЛИСТОВ МЧС РОССИИ | Опубликовать статью ВАК, elibrary (НЭБ)

К ВОПРОСУ СОЗДАНИЯ ЦИФРОВОЙ ОБРАЗОВАТЕЛЬНОЙ СРЕДЫ ДЛЯ ОБУЧЕНИЯ МАТЕМАТИКЕ
В ПРОЦЕССЕ ПОДГОТОВКИ СПЕЦИАЛИСТОВ МЧС РОССИИ

Научная статья

Трофимец Е.Н.*

ORCID: 0000-0003-4873-2801,

Санкт-Петербургский университет ГПС МЧС России, Санкт-Петербург, Россия

* Корреспондирующий автор (ezemifort[at]inbox.ru)

Аннотация

Статья посвящена основным элементам информационно-аналитической модели обучения математическим дисциплинам. Аргументировано, что одним из ключевых элементов информационно-аналитической модели является математическое моделирование с использованием инструментальных программных средств в образовательном процессе. В данной работе рассматривается применение компьютерной системы MathCad при изучении темы «Операторы дифференцирования». Приведен алгоритм решения практико-ориентированной задачи и ее анализ. Показано аналитическое и графическое решения. Описаны вычислительные блоки MathCad в процессе применения операторов дифференцирования. Обосновано использование пакетов прикладных программ в условиях цифровизации математического образования.

Ключевые слова: цифровизация, математическое образование, операторы дифференцирования.

ON THE ISSUE OF CREATING A DIGITAL EDUCATIONAL ENVIRONMENT FOR TEACHING MATHEMATICS IN THE PROCESS OF TEACHING TO THE SPECIALISTS OF EMERCOM 

Research article

Trofimets E.N.*

ORCID: 0000-0003-4873-2801,

Saint-Petersburg University of the State Fire Service of the EMERCOM of Russia, Saint Petersburg, Russia

* Corresponding author (ezemifort[at]inbox.ru)

Abstract

The article discusses the key elements of the information and analytical model of teaching mathematical disciplines. It is argued that one of the key elements of the information and analytical model is mathematical modeling using instrumental software tools in an educational process. The article discusses the use of the MathCad software in studying the topic of differential operators. It also provides an algorithm for solving a practice-oriented problem and its analysis and shows analytical and graphical solutions. The study describes computational blocks of MathCad in the process of applying differential operators and justifies the use of application software packages in the context of digitalization of mathematical education.

Keywords: digitalization, mathematical education, differentiation operators.

Введение

В настоящее время в связи с резким возрастанием объема информации, которую должен получить, понять, осознать и в дальнейшем суметь применить в своей профессиональной деятельности курсант МЧС России, одной из основных задач является поиск оптимальных путей обучения. В высших учебных заведениях МЧС России в числе значимых дисциплин, с которых начинается процесс обучения, является высшая математика. Именно, от качества математической подготовки в значительной степени зависит уровень сформированности профессиональных компетентностей будущего специалиста в области противопожарной службы и гражданской защиты [1], [3], [5].

В образовательном процессе математической подготовки XXI века используется информационно-аналитическая модель обучения (ИАМО).

В процессе использования ИАМО очень важно помнить, что при переходе от одной темы к другой, надо учитывать не только факторы сжатия информации, из которых следует уменьшение объема информации и повышение емкости получаемых знаний, но и учитывать необходимость защиты курсантов от информационной нагрузки и перегрузки. Это достигается за счет специальной организации базы знаний, доступ к которой возможен в любой точке траектории обучения на текущем уровне.

Одним из ключевых элементов информационно-аналитической модели является математическое моделирование с использованием инструментальных программных средств в образовательном процессе специалистов МЧС России.

В процессе моделирования представление знаний связано со знаково-символической деятельностью и характеризуется структурированностью, связностью и активностью представления информации.

Модель должна адекватно отражать основные, главные черты исследовательской деятельности будущего специалиста МЧС России и должна быть описана математически; кроме того, необходимо учесть роль каждого определяющего структуру элемента, его функции и характеристики.

Поэтому актуальной является проблема такой организации процесса обучения дисциплинам математического цикла, когда представления, возникающие в мышлении обучаемых, отражают основные, существенные, ключевые стороны предметов, явлений и процессов, в том числе посредством адекватного моделирования математического знания.

При этом особую значимость приобретают модели, фиксирующие процедуру математических действий в процессе исследовательской активности с использованием пакетов прикладных программ.

Из вышесказанного, следует, что в процессе подготовки специалистов МЧС России в рамках цифровизации образовательной среды актуально использовать на занятиях по математике пакеты прикладных программ при решении практико-ориентированных задач [2], [4], [7].

В данной работе фокус внимания смещен на применение компьютерной системы MathCad при изучении темы «Операторы дифференцирования».

Операторы дифференцирования служат точкой опоры всех динамических процессов. Особенно важны операторы дифференцирования инженерам: пожарной безопасности, техносферной безопасности, судебным экспертам при изучении процессов развития и тушения пожаров.

Для грамотного применения операторов дифференцирования в процессе решения профессиональных задач необходимо овладеть технологией дифференцирования и ее применением к практико-ориентированным задачам. Базовые знания дифференцирования с применением пакетов прикладных программ являются вектором направления и исследования динамических, ситуационных процессов: прогнозирование сценариев развития пожара, определение оптимальной пожарной тактики.

Для совершенствования образовательного процесса математическим дисциплинам с использованием пакетов прикладных программ необходима информационно-аналитическая модель обучения.

Одним из ключевых элементов, составляющих информационно-аналитическую модель обучения, является элемент интеграции математических и профессиональных знаний с применением пакетов прикладных программ.

Разработка новых методико-методологических подходов к организации обучения математическим дисциплинам в век информационных технологий своевременна и актуальна.

Знания и умения по технологии дифференцирования достигаются в процессе решения практико-ориентированных задач.

Постановка практико-ориентированной задачи (ПОЗ).

ПОЗ. Найдите угол между параболами  в точке их пересечения. Постройте графики парабол и касательных к ним в точке пересечения.

Замечание: напомним, что углом между двумя кривыми  и в точке их пересечения M₀(x₀, y₀) называется угол между касательными к этим кривым в точке M₀, тангенс которого находится по формуле:

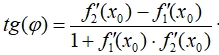
Алгоритм решения ПОЗ на рабочем листе MathCad.

1. Задайте функции 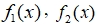, и найдите координаты точки их пересечения M₀.

Для того чтобы найти координаты точки M₀, необходимо решить систему нелинейных уравнений:

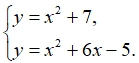
В Mathcad для решения систем линейных и нелинейных уравнений можно воспользоваться вычислительным блоком Given/Find (Дано/Найти). Блок Given/Find состоит из трех частей, идущих последовательно друг за другом:

• Given – ключевое слово;
• система, записанная логическими операторами в виде равенств и, возможно, неравенств;
• Find(x₁, … , x_n) – встроенная функция для решения системы уравнений относительно переменных x₁, … , x_n.

Особенность использования блока Given/Find состоит в том, что для записи уравнений используется не оператор численного вычисления (клавиша <=> на клавиатуре, а оператор булевого равенства, расположенный на панели Булева алгебра (или комбинация клавиш на клавиатуре). Для вставки функции Find необходимо выполнить цепочку команд Вставка – Функция – Решение уравнений – Find.

На рис. 1 представлены заданные функции , а также вычислительный блок Given/Find.

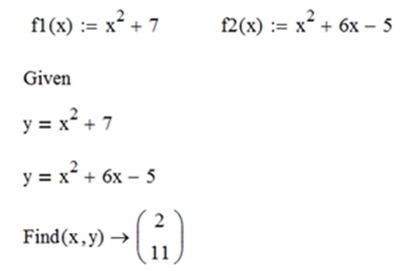
Рис. 1 – Нахождение координат точки M₀

Таким образом, точка M₀ имеет координаты (2; 11).

2. Вычислите производные функций 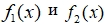 в точке x₀ = 2 (рис. 2).

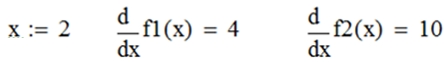
Рис. 2 – Вычисление  

 

3. Для нахождения угла между параболами воспользуйтесь функцией atan(z), которая вычисляет арктангенс, т.е. величину угла (в радианах), тангенс которого равен z. Для вставки функции atan выполните цепочку команд Вставка – Функция – Тригонометрические – atan. После ввода функции нажмите на клавиатуре клавишу <=> (равно) – результат представлен на рис. 3 (выражение в скобках является тангенсом угла φ).

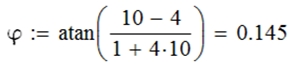
Рис. 3 – Вычисление угла φ (в радианах)

 

Как уже было отмечено, функцией atan вычисляет величину угла в радианах. Для перехода к градусам воспользуемся удобной функциональной возможностью Mathcad по заданию единиц измерения размерных величин. Для этого щелкните по блоку с функцией atan и поставьте курсор в конец блока после черного маркера (рис. 4).

Рис. 4 – Подготовка к вводу единиц измерения угла φ

 

Выполните цепочку команд Вставка – Единица измерения. В окне Вставка единицы измерения в качестве размерности выберите угол, а в качестве единицы измерения – градусы (рис. 5).

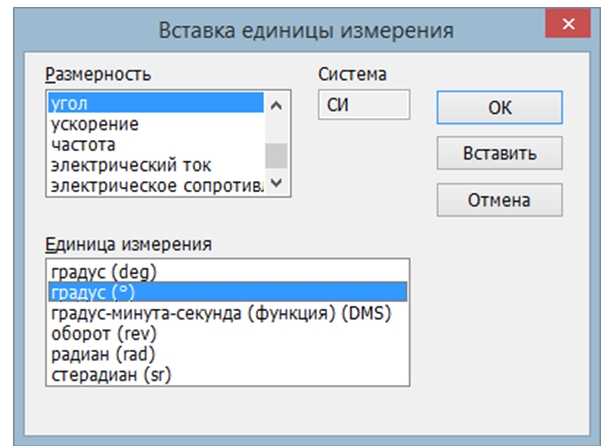
Рис. 5 – Окно «Вставка единицы измерения»

 

Результат представлен на рис. 6.

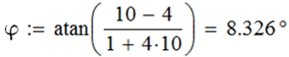
Рис. 6 – Вычисление угла j (в градусах)

 

4. Для построения графиков функций 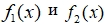 переопределите их через другую переменную, например z (рис. 7).

 

Рис. 7 – Задание функций  и  через переменную z

 

5. Запишите самостоятельно уравнения касательных 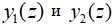, также используя переменную z.
6. Постройте графики функций 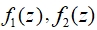 и касательных  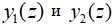(рис. 8).

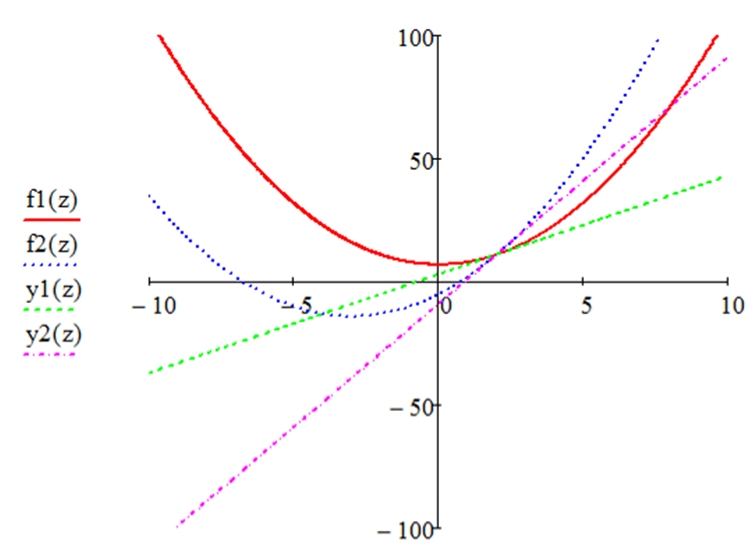
Рис. 8 – Графики функций и касательных

 

Заключение

Использование пакетов прикладных программ в условиях цифровизации математического образования способствует повышению уровня математической подготовки будущих специалистов МЧС России, а также формированию и развитию профессиональной мотивации. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Artamonov V.S. Information systems and processes in the analytical training of management scholars /
   V.S. Artamonov, A.Y. Ivanov, S.V. Sharapov et al. // Espacios, Vol. 38 (N 25), 2017, P. 18.
2. Батьковский А.М. Системы поддержки принятия решений с модулями прикладных математических моделей и методов / А.М. Батьковский, В.Я. Трофимец // Вопросы радиоэлектроники. – 2015. – № 9. – С. 253-275.
3. Булгаков С.В. Применение мультиагентных систем в информационных системах / С.В. Булгаков // Перспективы науки и образования. – 2015. – № 5 (17). – С. 136-140 с.
4. Трофимец В.Я. Оптимизация в Excel: учеб. пособие / В. Я. Трофимец, Е. Н. Трофимец. – Ярославский государственный технический университет, Ярославль, 2008. – 104 с.
5. Трофимец Е.Н. Информационные технологии математического моделирования в экономических вузах /
   Е.Н. Трофимец // Образовательные технологии и общество. 2012. Т. 15. № 1. С. 414-423.
6. Трофимец Е.Н. Концептуальная модель научно-методического аппарата решения профессионально-ориентированных экономических задач. / Е.Н. Трофимец // Вестник Российского университета дружбы народов. Серия «Информатизация образования». 2009. № 4. С. 107-117.
7. Balychev S. Situational modeling of transportation problems: applied and didactic aspects / S. Balychev, A. Batkovskiy, P. Kravshuk et al. // Espacios, Vol. 39 (N 10), 2018. – P. 27.
8. Трофимец Е.Н. Анализ содержания информационно-аналитической подготовки специалистов экономического профиля / Е.Н. Трофимец, А.А. Трофимец // Технические и естественные науки; безопасность: информация, техника, управление. Санкт-Петербург, 24–28 февраля 2021 года. Сборник статей по материалам конференций ГНИИ «НАЦРАЗВИТИЕ», 2021. Изд-во: ГНИИ “Нацразвитие”. Санкт-Петербург, 2021. – С. 94-96.
9. Трофимец Е.Н. Компьютерное моделирование в образовательном процессе студентов-экономистов /
   Е.Н. Трофимец // Информатика и образование 2008. № 7. С. 118-119.
10. Трофимец Е.Н. Дидактические аспекты применения технологии компьютерного моделирования в образовательном процессе студентов-экономистов / Е.Н. Трофимец, В.Я. Трофимец // Институциональные основы экономики опережающего развития. Материалы международной научно-практической конференции. под науч. ред. Л.Г. Батраковой. 2019. Изд-во: Ярославский государственный педагогический университет им. К.Д. Ушинского. –
    С. 277-282.

Список литературы на английском языке / References in English

1. Artamonov V.S. Information systems and processes in the analytical training of management scholars /
   V.S. Artamonov, A.Y. Ivanov, S.V. Sharapov et al. // Espacios, Vol. 38 (N 25), 2017, P. 18.
2. Batkovsky A.M. Sistemy podderzhki prinjatija reshenijj s moduljami prikladnykh matematicheskikh modelejj i metodov [Decision support systems with modules of applied mathematical models and methods] / A. M. Batkovsky, V. Ya. Trofimets // Voprosy radioehlektroniki [Issues of Radioelectronics]. – 2015. – No. 9. – pp. 253-275 [in Russian]
3. Bulgakov S. V. Primenenie mul’tiagentnykh sistem v informacionnykh sistemakh [Application of multi-agent systems in information systems] / S. V. Bulgakov // Perspektivy nauki i obrazovanija [Prospects of science and education]. – 2015. – № 5 (17). – pp. 136-140 p. [in Russian]
4. Trofimets V. Ya. Optimizacija v Excel: ucheb. posobie [Optimization in Excel: A Manual] / V. I. Trofimets,
   E. N. Trofimets. – Yaroslavl State Technical University, Yaroslavl, 2008. – 104 p. [in Russian]
5. Trofimets E. N. Informacionnye tekhnologii matematicheskogo modelirovanija v ehkonomicheskikh vuzakh [Information technologies of mathematical modeling in economic universities] / E. N. Trofimets // Obrazovatel’nye tekhnologii i obshhestvo [Educational technologies and society]. 2012. Vol. 15. No. 1, pp. 414-423 [in Russian]
6. Trofimets E. N. Konceptual’naja model’ nauchno-metodicheskogo apparata reshenija professional’no-orientirovannykh ehkonomicheskikh zadach [Conceptual model of the scientific and methodological apparatus for solving professionally oriented economic problems] / Vestnik Rossijjskogo universiteta druzhby narodov. Serija «Informatizacija obrazovanija [Bulletin of the Peoples ‘ Friendship University of Russia. Series: “Informatization of education”]. 2009. № 4, pp. 107-117.
   [in Russian]
7. Balychev S. Situational modeling of transportation problems: applied and didactic aspects / S. Balychev, A. Batkovskiy, P. Kravshuk et al. // Espacios, Vol. 39 (N 10), 2018. – P. 27.
8. Trofimets E. N. Analiz soderzhanija informacionno-analiticheskojj podgotovki specialistov ehkonomicheskogo profilja [Analysis of the content of information and analytical training of economic specialists] / E. N. Trofimets, A. A. Trofimets // Tekhnicheskie i estestvennye nauki; bezopasnost’: informacija, tekhnika, upravlenie. Sankt-Peterburg, 24–28 fevralja 2021 goda. Sbornik statejj po materialam konferencijj GNII «NACRAZVITIE» [Technical and natural sciences; security: information, technology, management. St. Petersburg, February 24-28, 2021. Collection of articles based on the materials of the conferences of the State Research Institute “Natsrazvitie”], 2021. Publishing house: GNII “Nacrazvitie”. St. Petersburg, 2021. pp. 94-96 [in Russian]
9. Trofimets E. N. Komp’juternoe modelirovanie v obrazovatel’nom processe studentov-ehkonomistov [Computer modeling in the educational process of economics students] / E. N. Trofimets // Informatika i obrazovanie [Informatics and education] 2008. No. 7, pp. 118-119 [in Russian]
10. Trofimets E. N. Didakticheskie aspekty primenenija tekhnologii komp’juternogo modelirovanija v obrazovatel’nom processe studentov-ehkonomistov [Didactic aspects of the application of computer modeling technology in the educational process of economics students] / E. N. Trofimets, V. Ya. Trofimets // Institucional’nye osnovy ehkonomiki operezhajushhego razvitija. Materialy mezhdunarodnojj nauchno-prakticheskojj konferencii [Institutional foundations of the economy of advanced development. Proceedings of the international scientific and practical conference]. Edited by L. G. Batrakova. 2019. Publishing house: Yaroslavl State Pedagogical University named after K. D. Ushinsky, pp. 277-282 [in Russian]