ОБОБЩЕНИЕ ДАННЫХ ПО АЭРОДИНАМИЧЕСКОМУ СОПРОТИВЛЕНИЮ ПАКЕТОВ ВИНТООБРАЗНЫХ ТРУБ | Опубликовать статью РИНЦ

Письменный Е. Н.¹, Рева С. А.², Терех А. М.³, Руденко А. И.⁴

¹Доктор технических наук, профессор, ² Инженер, ³Кандидат технических наук, старший научный сотрудник, ⁴Кандидат технических наук, доцент, Национальный технический университет Украины, “Киевский политехнический институт”

ОБОБЩЕНИЕ ДАННЫХ ПО АЭРОДИНАМИЧЕСКОМУ СОПРОТИВЛЕНИЮ ПАКЕТОВ ВИНТООБРАЗНЫХ ТРУБ

Аннотация

Предложена обобщенная зависимость для расчета аэродинамического сопротивления шахматных пакетов однозаходных винтообразных труб с равноразвитой поверхностью в диапазоне чисел Рейнольдса (5…70)·10³. Показано, что коэффициент C_s и показатель степени n при числе Рейнольдса в уравнении подобия зависит от геометрических характеристик труб и пакетов.

Ключевые слова: винтообразная труба, пакет, обобщение, расчет, равноразвитая поверхность, аэродинамическое сопротивление.

Pism’mennyi E. N.¹, Reva S. A.², Terekh A. M.³, Rudenko A. I.⁴

¹Doctor of technical science, professor, ²Engineer, ³Candidate of technical science, senior researcher, ⁴Candidate of technical science, associate professor.

National Technical University of Ukraine “Kiev Polytechnic Institute”

THE GENERALIZED DATA OF AERODYNAMIC DRAG OF THE STAGGERED BUNDLES OF SCREW-SHAPED TUBES

Abstract

The generalized dependence for calculation of aerodynamic drag of the staggered bundles of screw-shaped tubes with equal size surface in the range of numbers of Reynolds (5…70) 10³ is suggested. It is shown that the coefficient of C_s and n exponent at Reynolds’s number in the equation of similarity depends on geometrical characteristics of tubes and bundles.

Keywords: screw-shaped tube, bundles, generalization, calculation, equal size surface, aerodynamic drag.

1. Введение

В работе представлены обобщенные зависимости для расчета коэффициентов аэродинамического сопротивления шахматных пакетов винтообразных труб. Предложенные зависимости могут быть использованы при проектировании компактных теплообменников типа “газ – газ” в широких интервалах изменения геометрических характеристик труб,  пакетов и режимных параметров.

2. Объект исследований

Для исследований аэродинамического сопротивления шахматных пакетов винтообразных труб [1,2] использовались модели труб, которые изготовлены из алюминиевого сплава Д16-т (рис.1). Основные геометрические характеристики исследованных труб приведены в табл.1.

Рис. 1 – Модели однозаходных винтообразных труб

а) модель трубы типа 1; б) модель трубы типа 2

Таблица 1 – Геометрические характеристики моделей труб

Тип труб	l, мм	D, мм	d, мм	t, мм	h, мм	y	H1пм, м2/м
1	140	38	28	12	5	1,163	0,1388
2	140	38	31	8	3,5	1,241	0,1481

 

3. Методика исследований аэродинамического сопротивления

Исследование аэродинамического сопротивления шахматных пакетов винтообразных труб с равноразвитой поверхностью при поперечном их обтекании воздушным потоком осуществлялось на экспериментальной установке, представляющей собой аэродинамическую трубу разомкнутого типа прямоугольного пересечения по методикам, которые детально описаны в работе [3]. Исследовано два типа труб, отличающиеся геометрическими характеристиками (табл.1) из которых комбинировались пакеты( рис.2). Всего експериментами охвачены 32 пакета, которые имели различные шаговые характеристиками S₁, S₂ и приведенные длины H/F [4]. Пакет, в зависимости от шаговых характеристик, состоял из 3-5 труб в одном поперечном ряду (Z₁ = 3-5) и 6 поперечных рядов (Z₂=6).

4. Обобщение опытных данных

 

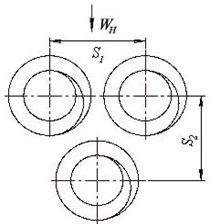
Рис. 2 – Пакет однозаходных винтообразных труб  шахматной компоновки

Предварительный анализ полученных данных, а также существующий в литературе [4-8] опыт обобщения результатов, исследования аэродинамического сопротивления разнообразных теплообменных поверхностей, показали, что при обработке экспериментальных данных по сопротивлению пакетов ребристых труб в качестве основного параметра учитывающего влияние геометрии оребренных труб целесообразноиспользовать приведенную длину H/F [7]. Как идентификатор размещения труб в пакете использовалось отношение поперечного шага S₁ к продольному S₂. Параметр размещения труб S₁/S₂ имеет преимущества по сравнению с относительными шагами S₁/d₁, S₂/d₂, позволяющий сократить число переменных в обобщенных формулах, увеличивает их точность и универсальность.

Полученные опытные данные также свидетельствуют про целесообразность обобщения степенными зависимостями вида

         (1)

На рис.3,4 показаны зависимости значений показателя степени n при числе Рейнольдса и коэффициента C_s от S₁/S₂. Расслаивающим параметром представленных значений является приведенная длина H/F. Изменение значений n и C_s происходит, как в диапазоне одинаковых значений H/F при S₁/S₂=var, так и для пакетов с одинаковыми параметрами размещения S₁/S₂ при H/F=var.

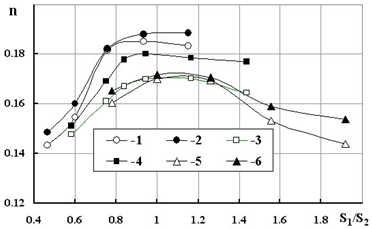
Рис.3 – Зависимость показателя степени n в формуле (4) от S₁/S₂:

1 – H/F=15,42; 2 – H/F=19,75; 3 – H/F=7,12;

4 – H/F=8,23; 5 – H/F=3,75; 6 – H/F=4,17

Кривые на рис. 3,4 имеют экстремумы функций в области значений S₁/S₂=(0,8-1,0). Таким образом, можно констатировать, что параметры H/F и S₁/S₂ есть равноправными факторами, которые учитывают влияние геометрии размещения труб в пакете, а также геометрии самих труб на потери давления в пакете.

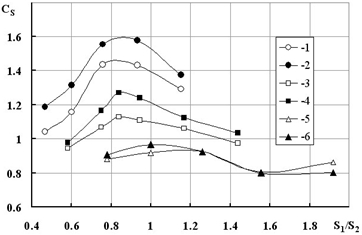
Рис.4 – зависимость коэффициента C_s в формуле (4) от S₁/S₂:

1 – H/F=15,42; 2 – H/F=19,75; 3 – H/F=7,12;

4 – H/F=8,23; 5 – H/F=3,75; 6 – H/F=4,17

Вследствие чего, расчетные зависимости для n и C_s можно представить в виде:

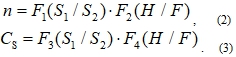
Определение функции F₁(S₁/S₂) а также функции F₃(S₁/S₂) проводилось с помощью математической обработки графических зависимостей изображенных на рис. 3,4. Математическое описание этих функций имеет следующий вид:

где К₁, К₂, К₃, К₄ – эмпирические коеффициенты.

Для определения функций, что учитывают влияние приведенной длины в формуле (4,5) были построены графики (рис. 5) зависимостей вида n/F₁(S₁/S₂) и C_s/ F₃(S₁/S₂) от приведенной длины H/F.

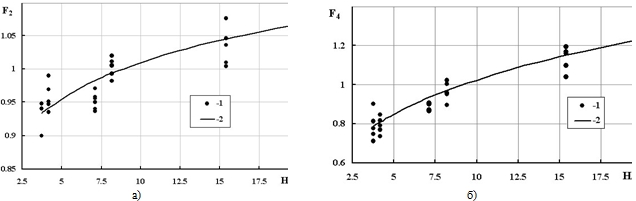
Рис.5 – Зависимость функций а) – F₂(H/F), б) – F₄(H/F) от H/F:

1 – опытные данные; 2 – расчетная кривая

Математическая обработка полученных значений показала, что они довольно хорошо аппроксимируются степенными функциями. Вследствие чего функции, которые учитывают влияние приведенной длины, можно записать в таком виде

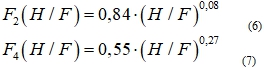
Таким образом, уравнения для расчета значений показателя степени n при числе Рейнольдса и коэффициента C_s в формуле (4) примут вид

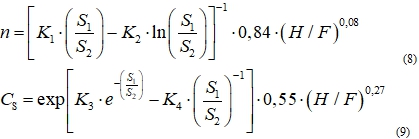
Точность расчетных значений для n и C_s составляет ±(4-5)% и ±(12-15)% соответственно.

Суммарная погрешность расчетных формул оценивалась прямым сопоставлением опытных и расчетных за формулами (1),(8),(9) чисел Ейлера при фиксированных значений чисел Re_D=5·10³ и 5·10⁴. Разброс опытных данных относительно расчетных линий аэродинамического сопротивления составляет не больше ±15% для всех исследуемых пакетов труб.

     5. Выводы

Полученные обобщенные зависимости для определения коэффициентов аэродинамического сопротивления можно применять в диапазоне чисел Рейнольдса (5…70)·10³ для поверхностей теплообмена состоящих с однозаходных винтообразных труб.

С помощью обобщенной зависимости можно определить наилучшую поверхность среди множества вариантов с различными геометрическими характеристиками как труб, так и пакетов.

Полученные опытные данные, а также расчетные зависимости могут лечь в основу методики аэродинамического расчета теплообменных аппаратов с пакетами винтообразных труб с равноразвитой поверхностью.