О НАИЛУЧШЕЙ АППРОКСИМАЦИИ АБСОЛЮТНО МОНОТОННЫМИ ФУНКЦИЯМИ НА ПОЛУОСИ | Опубликовать статью РИНЦ

О НАИЛУЧШЕЙ АППРОКСИМАЦИИ АБСОЛЮТНО МОНОТОННЫМИ ФУНКЦИЯМИ НА ПОЛУОСИ

Научная статья

Федоров В.М. *

ORCID: 0000-0002-4586-6591,

Московский Государственный Университет им. М.В. Ломоносова, Москва, Россия

* Корреспондирующий автор (vferdorov[at]rambler.ru)

Аннотация

Основной  результат статьи  (теорема 2) состоит в том,  что в пространстве C(I) непрерывных функций на отрезке I = [0, ∞] конус K⊂C (I), состоящий из абсолютно монотонных функций является чебышевским, т.е. для каждой непрерывной функции f∈C (I) найдется единственная абсолютно монотонная функция φ∈K наилучшего равномерного приближения на отрезке I. При этом в доказательстве будет использован специальный критерий единственности наилучшего приближения клином (теорема 1). Этот критерий может быть использован при доказательстве единственности наилучшего приближения для других конусов, состоящих из непрерывных функций.

Ключевые слова: наилучшее равномерное приближение, опорный клин, опорная плоскость, непрерывная функция, абсолютно монотонная функция.

ON THE BEST APPROXIMATION BY ABSOLUTELY MONOTONIC FUNCTIONS ON SEMIAXIS

Research article

Fedorov V.M. *

ORCID: 0000-0002-4586-6591,

Lomonosov Moscow State University, Moscow, Russia

* Corresponding author (vferdorov[at]rambler.ru)

Abstract

The main result of the paper (Theorem 2) is that in the space C(I) of continuous functions on the interval I = [0, ∞], the cone K⊂C (I) consisting of absolutely monotone functions is Chebyshev, that is, for each continuous function f∈C (I) there is a unique absolutely monotonic function φ∈K of the best uniform approximation on the interval I. In the proof, we use a special criterion for the uniqueness of the best approximation by the wedge (Theorem 1). This criterion can be used in proving the uniqueness of the best approximation for other cones consisting of continuous functions.

Keywords: best uniform approximation, reference wedge, reference plane, continuous function, absolutely monotonic function.

Введение

Множество в нормированном пространстве  называется чебышевским, если оно обладает свойствами существования и единственности для наилучшего приближения любого элемента этим множеством.  Доказательство этих свойств для бесконечномерных  множеств в нормированном пространстве и, в частности, в пространстве непрерывных функций, является трудной математической задачей. Вначале мы рассмотрим задачу наилучшего приближения клином в абстрактном нормированном пространстве.

Пусть  E   нормированное пространство над полем действительных чисел . Непустое подмножество  называется клином, если  [1, c. 39]. Клин  называется конусом, если не содержит нетривиальных линейных подпространств, т.е. пересечение  равно нулю. Обозначим через  полярный* клин (конус) в сопряженном пространстве E* к пространству E [1, c. 33]. Если клин   является подпространством, то полярный* клин  совпадает с аннулятором*  (см. также [2, c. 198] и [3, c. 160]).

Экстремальные множества функционала  и вектора  задаются  формулами  замкнутые единичные шары в   соответственно. Если  не пусто, то функционал называется опорным. Обозначим через    опорный клин в точке , т.е. коническую оболочку  множества  опорную плоскость в точке , т.е. наибольшее действительное линейное подпространство, содержащееся в опорном клине.

Лемма 1

Замкнутый клин  в нормированном пространстве E тогда только тогда обладает свойством единственности наилучшего приближения, когда для любой точки p ∈ K и для каждого ненулевого опорного функционала пересечение   равно нулю.

Доказательство. Необходимость. Пусть . Допустим, что множество  имеет две различные точки . В силу его  выпуклости  . Поэтому , т.е. величина  совпадает с расстоянием  от точки  .

Следовательно, мы имеем равенство . Поскольку выполняется включение  при достаточно малых t > 0, то клин K в пространстве E не обладает свойством единственности наилучшего приближения. Получили противоречие.

Достаточность. Если клин K не обладает свойством единственности, то в силу  выпуклости существуют  . Поскольку  образует крайнее множество  клина . Полагая. По теореме отделимости выпуклых множеств [1, стр. 42] существует . Поскольку  является крайним множеством шара S, то . Таким образом,  , что противоречит нашему предположению.

Теорема 1

Замкнутый клин  в пространстве C(T) непрерывных  функций на компакте T в том и только в том случае не обладает свойством единственности наилучшего приближения,  когда существуют  точка  ,  ненулевой опорный функционал  и ненулевая функция , где  носитель α, а  множество нулей φ.

 Доказательство. Необходимость. В силу леммы 1 существуют точка   и ненулевой опорный функционал , т.ч.  не равно нулю. Обозначим через μ представляющую меру функционала α [1, c. 55]. Мы можем считать, что  . Тогда существуют две различные функции . Поэтому  . Отсюда получим  при п.в.  и, следовательно, имеем . Таким образом, в силу непрерывности   выполняется включение .

Достаточность. Рассмотрим ненулевой опорный функционал  и  ненулевую функцию . Пусть . Поскольку α является опорным, то существует . Определим непрерывную функцию . Тогда имеют место неравенства . Так как непрерывная функция . Поэтому получаем . Поскольку , то  и, следовательно, функция .  Таким образом, в силу леммы 1 клин  не обладает свойством единственности наилучшего приближения.

Рассмотрим в пространстве  непрерывных функций на отрезке , состоящий из ограниченных абсолютно монотонных функций, представимых интегралом Лапласа Стилтьеса [4, c. 18]

где  ограниченная неубывающая функция на отрезке I. Если предположить, кроме того, что  является непрерывной слева и , то соответствие между неубывающими функциями  и абсолютно монотонными  функциями  будет взаимно однозначным. Поскольку по теореме Бернштейна функция абсолютно монотонна в том и только в том случае, когда она удовлетворяет некоторой системе неравенств конечных разностей [5, c. 252], то конус  является по точечно замкнутым и, следовательно, в силу теоремы Мазура он будет равномерно  замкнутым в пространстве C(I) [6, c. 457].

Спектром  неубывающей функции  называется множество точек роста этой функции, т.е. таких , что в любой ее окрестности найдутся точки , для которых функция  строго возрастает, т.е.  соответственно. Спектр для произвольной функции ограниченной вариации  [1, c. 56] определяется спектром вариации . По определению спектр абсолютно монотонной функции  совпадает со спектром соответствующей ей неубывающей функции .

Лемма 2

Опорная плоскость  конуса абсолютно монотонных функций в точке  состоит из функций  функция ограниченной вариации, т.ч. , а P(t) — неубывающая функция на отрезке I, соответствующая абсолютно монотонной функции p ∈ K.

Доказательство. Пересечение  есть наибольшее выпуклое подмножество K, имеющее точку  своей относительно окруженной точкой [2, c. 110]. Поэтому множество  образует замкнутую грань конуса K  и его линейная оболочка . Если неубывающая функция является суммой  двух неубывающих функций, то в силу экстремального свойства грани соответствующая ей абсолютно монотонная функция  в том и только в том случае принадлежит , когда . Следовательно, при всех  этой грани  принадлежат функции, представимые в следующем виде:

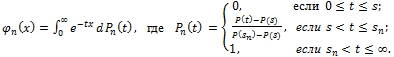
Если  является точкой роста справа для P, то, переходя к пределу при , получим, что . Поэтому некоторая последовательность выпуклых комбинаций функций  сходится по норме к функции  (см. [6, c. 457] или [7, c. 216]). Поэтому имеет место .  Аналогичное утверждение справедливо также для точек роста слева. Заметим, что . В самом деле, так как спектр замкнут, то существует окрестность . В этой окрестности функция является константой и не может быть суммой двух возрастающих функций, отличных от констант. Таким образом, замкнутая коническая оболочка  функций  , где , совпадает с замкнутой гранью  конуса K.

Теорема 2

Конус   абсолютно монотонных функций со спектром на отрезке   является чебышевским.

Доказательство. В начале докажем существование наилучшего приближения для любой функции. Выберем последовательность функций , и обозначим через  неубывающие функции на I, непрерывные слева и нормированные условием , соответствующие . Так как , то последовательность функций  равномерно ограничена и, следовательно, существует подпоследовательность ,  которая в каждой точке  сходится к неубывающей функции  (см. [8, c. 63] или [9, c. 207]). По теореме Хелли (см. [8, c. 65] или [9, c. 219]) абсолютно монотонные функции , соответствующие , сходятся в каждой точке  к абсолютно монотонной функции , соответствующей . Следовательно, имеет место неравенство  при всех . Отсюда вытекает равенство  и значит функция  является наилучшим приближением функции f.

Для доказательства единственности наилучшего приближения конусом K мы используем теорему 1. Допустим, что ненулевой опорный функционал  удовлетворяет условию  некоторая ненулевая функция. Каждая ненулевая функция, принадлежащая опорной плоскости , голоморфна в правой полуплоскости, при этом множество ее нулей на отрезке I не более, чем счётно, и не имеет предельных точек внутри этого отрезка. Пусть  обозначает множество нулей функции , упорядоченное в порядке возрастания. Поскольку носитель , то функционал  представляется в виде суммы абсолютно сходящегося ряда , где

 обозначает функционал Дирака с носителем в точке . Заметим, что по условию указанный функционал α аннулирует опорную плоскость  и  его норма определяется по формуле . Поэтому  в силу леммы 2 получим  при всех . Поскольку множество нулей  голоморфной функции  не более, чем счётно, и не содержит предельных точек внутри отрезка I, то этими же свойствами обладает и спектр  функции .

Если спектр  бесконечный, то последовательность чисел   будет иметь бесконечное число перемен знака [10, c. 60], что невозможно, так как функционал α является опорным. Пусть спектр  является конечным и состоит из m точек . Тогда последовательность  должна иметь, по крайней мере, m перемен знака и, следовательно, будет содержать, по крайней мере, m + 1 ненулевых чисел. Так как по лемме 2 ненулевая функция  имеет вид , то она должна иметь, по крайней мере, m + 1 нулей  на отрезке , что невозможно, поскольку  образует чебышевскую систему функций в  (см. [10, c. 54] и [11, c. 7]).

Заключение

Доказанная теорема 2 допускает обобщение на случай, когда конус K состоит не из всех абсолютно монотонных функций, а только из тех, у которых спектр содержится в заданном замкнутом подмножестве отрезка I. При этом для доказательства нам потребуется произвести совсем небольшие изменения в приводимом выше доказательстве теоремы 2.

Конфликт интересов Не указан.

Conflict of Interest None declared.