РАЗРАБОТКА СПОСОБОВ УВЕЛИЧЕНИЯ ДЛИНЫ ВОЛОКОННО-ОПТИЧЕСКОГО КАНАЛА СВЯЗИ КВАНТОВО-КРИПТОГРАФИЧЕСКОЙ СИСТЕМЫ | Опубликовать статью РИНЦ

РАЗРАБОТКА СПОСОБОВ УВЕЛИЧЕНИЯ ДЛИНЫ ВОЛОКОННО-ОПТИЧЕСКОГО КАНАЛА СВЯЗИ КВАНТОВО-КРИПТОГРАФИЧЕСКОЙ СИСТЕМЫ

Научная статья

Гончаренко Д.К.^1, *, Кулиш О.А.², Ивахненко А.В.³, Сидько Н.В.⁴

^{1, 2, 3, 4} Кубанский государственный университет, Краснодар, Россия

* Корреспондирующий автор (d_gon[at]list.ru)

Аннотация

В статье рассматривается способ увеличения длины волоконно-оптического канала связи квантово-криптографической системы. Так же  в статье рассматривается техническая сторона физического ограничения длины волоконно-оптической линии связи: проведен расчет, анализ и визуализация в виде графиков ключевых зависимостей  видности и квантового коэффициента ошибки от длины волоконной линии связи. Способом, рассматриваемым для увеличения длины волоконно-оптического канала связи, является установка квантового повторителя в квантовую криптосистему.

Ключевые слова: квантовые криптосистемы, передача данных,  волоконные линии связи, квантовые повторители.

DEVELOPMENT OF METHODS FOR INCREASING THE LENGTH OF A FIBER-OPTICAL COMMUNICATION CHANNEL OF A QUANTUM-CRYPTOGRAPHIC SYSTEM

Research article

Goncharenko D.K.^1, *, Kulish O.A.², Ivakhnenko A.V.³, Sidko N.V.⁴

^{1, 2, 3, 4} Kuban State University, Krasnodar, Russia

* Corresponding author (d_gon[at]list.ru)

Abstract

The article discusses the method for increasing the length of the fiber-optic communication channel of a quantum-cryptographic system. The article also discusses the technical side of the physical limitation of the length of the fiber-optic communication line: calculation, analysis and visualization in the form of graphs of the key dependences of the visibility and quantum error rate on the length of the fiber communication line were carried out. The installation of the quantum repeater in a quantum cryptosystem is considered as the method to increase the length of the fiber-optic communication channel.

Keywords: quantum cryptosystems, data transmission, fiber communication lines, quantum repeaters.

Введение

Динамичное развитие информационных технологий и систем удаленного управления существенно повышает потребность в новых принципах передачи, приема и обработки информации, в основу которых в ближайшем будущем могут лечь технологии квантовой информатики.

Перспективным подходом, обеспечивающим возможность передавать квантовые состояния в распределённых квантовых информационных системах в целях обеспечения безопасности передачи данных, является технология квантовой коммуникации.

Менее чем за 50 лет квантовая криптография прошла путь от идеи до воплощения в коммерческую систему квантового распределения ключей. Действующая аппаратура позволяет распределять ключи через квантовый канал на расстояние превышающие 100 км (рекорд 184 км), со скоростями достаточными для передачи ключей шифрования, но не достаточными для поточного шифрования магистральных каналов с помощью шифра Вернама.

Основные результаты

Технологическое применение квантовой криптографии существенным образом ограничивается экспоненциальным характером роста потерь в канале связи с увеличением расстояния передачи [9, С.157],[10, С.137].

В связи с этим были произведены расчеты, а так же были построены графики, визуализирующие ограниченность возможности применения квантовых систем.

Зависимость видности от длины волокна L определяется выражением

   (1)

где μ – среднее число фотонов исходящих от отправителя,  ‒ затухание волокна длиной L,  ‒ эффективность детектора получателя,  ‒ вероятность ошибочного отсчета на тактовый цикл. С подстановкой измеренных значений, которые включают в себя эффективность детектора и потери в аппарате получателя на уровне 5 дБ, принимая в расчет стандартное затухание волокна α = 0,2 дБ/км, может быть определено расчетное значение видности от длины волны [7, С.57].  Зависимость видности от длины волоконной линии показана на рисунке 1.

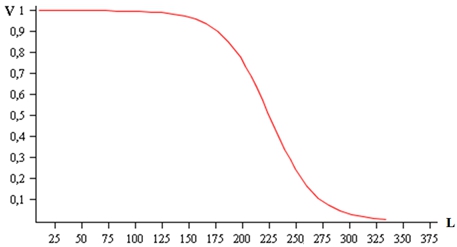
Рис. 1 – Зависимость видности от длины волоконной линии связи

 

Квантовый коэффициент   ошибки    может  быть  найден  из  значений  квантовой интерференционной видности. Для протокола ВВ84 квантовый коэффициент ошибки е может быть представлен как:

   (2)

Если QBER меньше, чем 11% отправитель и получатель могут сформировать общий ключ с минимальной информацией, доступной злоумышленнику, путем применения классических кодов, корректирующих ошибки. Коэффициент ошибки, вычисленный по формуле (2) с учетом значения = 8,5·10^-7 представлен на рисунке 2.

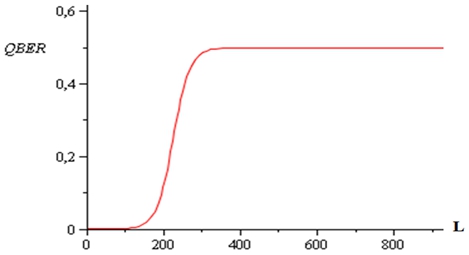
Рис. 2 – График зависимости коэффициента ошибки от длины волоконной линии связи

 

Из рисунка 1 видно, что при допустимом уровне видности 0,9 длина волоконной линии связи составит примерно 175 км. Из рисунка 2 следует, что допустимый квантовый коэффициент ошибки 11% достигается при длине волоконной линии связи около 200 км.

В случае классической коммуникации проблема потерь решается путем усиления сигнала в промежуточных узлах в процессе передачи, то есть использованием повторителей [4, С.188]. При передаче квантовой информации, однако, мы не можем “усилить” сигнал подобным образом из-за невозможности клонирования квантового состояния [2, С.123]. Тем не менее можно создать квантовый аналог повторителя, дающий возможность передачи квантовой информации на большие расстояния с помощью создания перепутанного состояния между отправителем и получателем [5, С.137],[6, С.772]. Это перепутывание затем может быть использовано при квантовой коммуникации, в частности, при квантовой телепортации или в протоколах квантового распределения ключа) [8, С.176]. Суть протокола квантового повторителя состоит в том, что между отправителем A и получателем B помещается ряд промежуточных узлов C₁, C₂, . . . , C_N−1, и изначально перепутывание создается между соседними из них (см. рисунок 3). Следующим шагом является создание на основе этого перепутывания перепутанного состояния между более далекими узлами — так называемый перенос перепутывания, или свопинг [1, С.50], [3, С.517]: если над кубитами в среднем из трех последовательных узлов произвести измерение,  проектирующее их на состояния Белла {|Φ⁺) , |Φ⁻⁾ , |Ψ⁺) , |Ψ⁻)}, а затем выполнить над крайними кубитами некоторые унитарные преобразования, зависящие от результата белловского измерения, то эти крайние кубиты (которые, заметим, никогда не взаимодействовали между собой) в результате окажутся в перепутанном состоянии (см. рис. 4). Проведение свопинга во всех узлах приведет к появлению требуемого перепутывания между узлами A и B.

Рис. 3 – Схема повторителя: между крайними узлами передачи A и B
помещаются промежуточные узлы C₁,C₂, . . . , C_N−1, между которыми создается перепутывание

 

Рис. 4 – Перенос перепутывания(свопинг): после создания перепутывания между соседними узлами (а) производится белловское измерение кубитов среднего узла (б), в результате чего крайние кубиты оказываются в перепутанном состоянии (в)

Заключение

В статье были рассчитаны, проанализированы и визуализированы в виде графиков ключевые зависимости видности и квантового коэффициента ошибки от длины волоконной линии связи. Была выявлена закономерная ограниченность дальности распространения сигнала, что обусловлено принципиальной невозможностью клонировать одиночный фотон и вытекающей из этого невозможности ретрансляции одиночного фотона с целью увеличения дальности его распространения. Так же было численно определено, при заявленных числовых характеристиках системы, максимально допустимое значение длины волоконной линии связи при сохранении приемлемых для передачи информации характеристик. Был рассмотрены классический способ увеличения длины волоконно-оптической линии связи с сохранением необходимых для передачи информации ключевых характеристик – установка квантовых повторителей.

Конфликт интересов Не указан.

Conflict of Interest None declared.