РАЗВИТИЕ МЕТОДА ДОПОЛНИТЕЛЬНОГО АРГУМЕНТА ДЛЯ СИСТЕМЫ НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Обзор
Аширбаева А.Ж.1, *, Садыкова Г.К.2
1 ORCID: 0000-0001-7706-0608,
1 Ошский технологический университет имени академика М.М. Адышева, Ош, Киргизия;
2 Ошский государственный университет, Ош, Киргизия
* Корреспондирующий автор (aijarkyn.osh[at]mail.ru)
Аннотация
В работе рассматривается начальная задача для систем уравнений и для решения задачи используется развитая методика дополнительного аргумента. Дается обзор известных результатов по рассматриваемому методу и на их основе обоснована степень актуальности исследуемой задачи. Поставленная начальная задача при использовании определенных классов функций сводится к системе интегральных уравнений. Такая развитая методика исследования могут применяться для доказательства существования решения новых видов векторно-матричных нелинейных уравнений.
Ключевые слова: система уравнений в частных производных, начальные условия, дополнительный аргумент, принцип сжимающих отображений.
DEVELOPMENT OF THE METHOD OF ADDITIONAL ARGUMENT FOR A SYSTEM OF NON-LINEAR DIFFERENTIAL EQUATIONS
Review
Ashirbaeva A.Zh.1, *, Sadykova G.K.2
1 ORCID: 0000-0001-7706-0608,
1 Osh Technological University named after M.M. Adyshev, Osh, Kyrgyz Republic;
2 Osh State University, Osh, Kyrgyz Republic
* Corresponding author (aijarkyn.osh[at]mail.ru)
Abstract
The paper considers the initial problem for systems of equations and uses the developed method of additional argument to solve the problem. A review of the known results on the method under consideration is presented, and the degree of relevance of the problem under study is substantiated on their basis. The stated initial problem is reduced to a system of integral equations when using certain classes of functions. This developed research technique can be used to prove the existence of a solution to new types of vector-matrix non-linear equations.
Keywords: a system of partial differential equations, initial conditions, an additional argument, the principle of contraction mappings.
Введение
В настоящее время метод дополнительного аргумента (МДА.) развивается для систем нелинейных уравнений в частных производных (в.ч.п.) [4, С. 410-414], [5, С. 17-23], [10, С. 111-115], [11, C.6-10].
В [1, С. 55-100] изложены в усовершенствованном виде основы МДА.
Аксиоматические основы МДА были выявлены в [2, С. 30-34].
В [3,С.37-40,8, С. 164] проведены компьютерные реализации МДА.
Построена общая схема МДА при исследовании широкого класса начальных задач для нелинейных операторно-дифференциальных уравнений [9, С. 12-24]. Показана применимость этой схемы для различных конкретных типов уравнений, второго, третьего, четвертого, а также произвольного порядка [9, С. 52-76], в конце обобщается для уравнений со многими пространственными переменными [9, С. 91-123].
Используя МДА исследованы уравнения типа Кортевега-де Фриза, а также нелинейные волновые уравнения. в ч.п. [6, С. 543-546], [7, С. 17-19].
Постановка задачи
Рассматривается начальная задача для системы дифференциальных уравнений в частных производных (ДУ в ЧП):
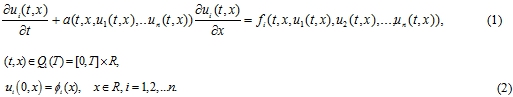
Используем классы функций, приведенные в [11] и следующее обозначение:
![]()
Использование МДА для систем ДУ в ЧП вида (1), рассматривается впервые.
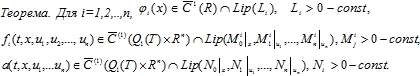
Тогда существует такое ![]() , что система ДУ в ЧП (1) с начальным условием (НУ) (2) имеет единственное решение в
, что система ДУ в ЧП (1) с начальным условием (НУ) (2) имеет единственное решение в ![]() .
.
Доказательство
Обозначим через ![]() пространство таких функций
пространство таких функций ![]() из ,что
из ,что
- ДУ в ЧП (1) с НУ (2) в пространстве эквивалентно
системе интегральных уравнений (ИУ):
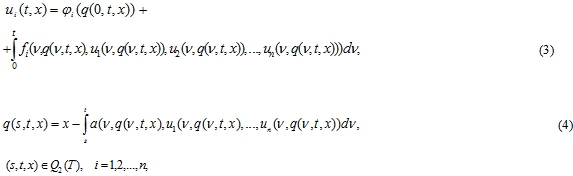
в пространстве ![]()
В самом деле, применяя МДА для ДУ в ЧП (1) с НУ (2), сводим задачу к системе ИУ (3), (4).
Пусть теперь ![]() – решение системы ИУ (3), (4).
– решение системы ИУ (3), (4).
Тогда ![]() удовлетворяют уравнению (1) и НУ (2).
удовлетворяют уравнению (1) и НУ (2).
В самом деле, из (3), (4) имеем:
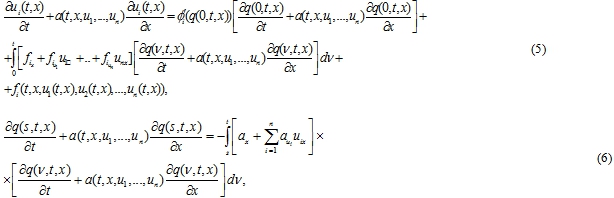
Для всякой функции ![]() из ИУ (6) имеем
из ИУ (6) имеем
![]()
Следовательно, из равенства (5) получается уравнение (1).
2. Система ИУ (3), (4) имеет единственное решение.
Преобразуем ИУ (3).
В системе ИУ (3), (4) как в [9] заменяем х на ![]() :
:
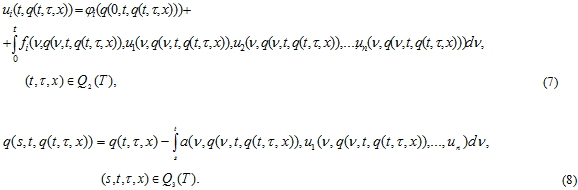
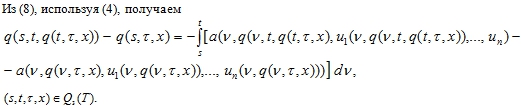
Отсюда имеем:
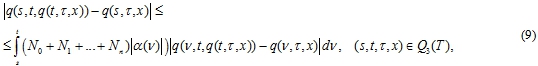
где ![]() – известная функция, определяемая по исходным данным.
– известная функция, определяемая по исходным данным.
Из интегрального неравенства (9) вытекает «тождество транзитивности», см. работу [9]:
![]() (10)
(10)
Тогда из системы ИУ (7), (8) учитывая (10), имеем:
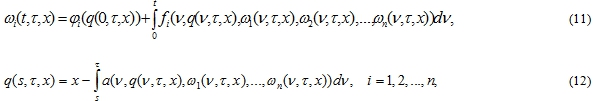
где обозначено
![]()
В системе ИУ (11),(12) приравнивая t на τ, получаем систему ИУ (3), (4). Учитывая обозначение (13), имеем ωi(t,t,x)=ui(t,x), i=1,2,…,n.
Итак достаточно доказать существование решение системы ИУ (11),(12).
Следовательно, используя МДА для ДУ в ЧП (1) с НУ (2), свели задачу к системе ИУ (11),(12).
Запишем эту систему (11),(12) в виде одного векторного уравнения, аналогично тому, как это делали в [11]
![]()
в котором ![]() – вектор-функция переменных
– вектор-функция переменных ![]() , компоненты вектор –функции:
, компоненты вектор –функции: ![]() , а компоненты оператора
, а компоненты оператора ![]() :
:
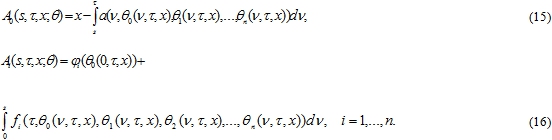
Поскольку пространство ![]() не является линейным, введем в нем метрику
не является линейным, введем в нем метрику ![]()
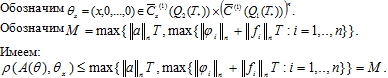
Покажем, что система уравнений (14)-(15)-(16) имеет в шаре ![]() пространства
пространства ![]() решение при некотором
решение при некотором ![]()
Справедливы следующие оценки
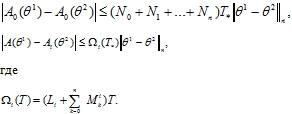
Отсюда следует, что оператор A при
![]()
осуществляет сжатое отображение шара ![]() на себя.
на себя.
Следовательно, по принципу сжимающих отображений уравнение (14) имеет одно и только одно решение. Таким образом, задача (1)-(2) также имеет единственное решение. Теорема доказана.
Заключение
Такая развитая методика исследования могут применяться для доказательства существования решения новых видов векторно-матричных нелинейных уравнений.
| Конфликт интересов
Не указан. |
Conflict of Interest
None declared. |
Список литературы / References
- Иманалиев М.И. Нелинейные интегро-дифференциальные уравнения с частными производными / М.И. Иманалиев. – Бишкек: Илим, 1992. – 112 с.
- Панков П.С. Квазикоммутативность дифференциальных операторов и ее приложение к обоснованию метода дополнительного аргумента / П.С. Панков, Т.М. Иманалиев // Исследования по интегро-дифференциальным уравнениям, Выпуск. 28. – Бишкек: Илим, 1999. – С. 30 – 34.
- Аширбаева А.Ж. Приближенное решение начальной задачи для нелинейных дифференциальных уравнений в частных производных второго порядка методом дополнительного аргумента / А.Ж. Аширбаева // Исследования по интегро-дифференциальным уравнениям. – Бишкек: Илим, 2014. – Выпуск. 46. – С. 37 – 40.
- Иманалиев М.И. К теории нелинейных интегро-дифференциальных уравнений в частных производных типа Уизема/ М.И. Иманалиев, С.Н. Алексеенко // Доклады Российской АН. – 1992. – Т. 323. – № 3. – С. 410 – 414.
- Иманалиев М.И. К теории почти солитонных решений нелинейного дифференциального уравнения в частных производных типа Кортевега-де Фриза четвертого порядка / М.И. Иманалиев, Т.М. Иманалиев, У.М. Иманалиев // Исследования по интегро-дифференциальным уравнениям. – Бишкек: Илим, 2003. – Выпуск 32. – С.17 – 23.
- Иманалиев М.И. К теории нелинейных уравнений с дифференциальным оператором типа полной производной по времени / М.И. Иманалиев, С.Н. Алексеенко // Доклады Российской АН. – 1993. – Т. 329. – № 5. – С. 543 – 546.
- Иманалиев М.И. К теории нелинейных дифференциальных уравнений в частных производных типа Кортевега – де Фриза / М.И. Иманалиев, П.С. Панков, Т.М. Иманалиев // Доклады Российской АН. – 1995. – Т. 342. – № 1. – С.17 – 19.
- Панков П.С. Приближенное решение начальной задачи для нелинейных дифференциальных уравнений в частных производных методом дополнительного аргумента / П.С.Панков, Т.М. Иманалиев, Г.М. Кененбаева // Юбилейная научная конференция, посвященная 50-летию развития математики в Академии наук Казахстана: Тезис, доклады – Алматы, 1995. – С. 164.
- Аширбаева А.Ж. Решение нелинейных дифференциальных и интегро-дифференциальных уравнений в частных производных высокого порядка методом дополнительного аргумента. – Бишкек: Илим, 2013. – 134 с.
- Иманалиев М.И. К теории систем нелинейных интегро-дифференциальных уравнений в частных производных типа Уизема / М.И. Иманалиев, С.Н. Алексеенко // Доклады АН. – 1992. – Т. 325. – № 6. – С.1111 – 1115.
- Аширбаева А.Ж. Решение системы нелинейных дифференциальных уравнений в частных производных первого порядка со многими переменными/А.Ж. Аширбаева, Ж.И. Мамбетов//Международный научно-исследовательский журнал. – 2018. – № 3 (69) – С.6-10.
Список литературы на английском языке / References in English
- Imanaliev M.I. Nelinejnye integro-differencial’nye uravnenija s chastnymi proizvodnymi [Nonlinear integral-differential equations with partial derivatives] / M.I. Imanaliev. – Bishkek: Ilim, 1992. – 112 p. [in Russian]
- Pankov P.S. Kvazikommutativnost’ differencial’nyh operatorov i ee prilozhenie k obosnovaniju metoda dopolnitel’nogo argumenta [Quasicommutativity of differential operators and its application to the justification of the method of an additional argument] / P.S. Pankov, T.M. Imanaliev // Investigations on integral-differential equations. Issue. 28. – Bishkek: Ilim, 1999. – P. 30 – 34. [in Russian]
- Ashirbaeva A.Zh. Priblizhennoe reshenie nachal’noj zadachi dlja nelinejnyh differencial’nyh uravnenij v chastnyh proizvodnyh vtorogo porjadka metodom dopolnitel’nogo argumenta [Approximate solution of the initial value problem for nonlinear partial differential equations of the second order by the method of an additional argument] / A.Zh. Ashirbaeva // nvestigations on integral-differential equations. – Bishkek: Ilim, 2014. – Issue. 46. – P. 37 – 40. [in Russian]
- Imanaliev M.I. K teorii nelinejnyh integro-differencial’nyh uravnenij v chastnyh proizvodnyh tipa Uizema [On the theory of nonlinear integral-differential partial differential equations of Whitham type]/ M.I. Imanaliev, S.N. Alekseenko // Reports of the Russian Academy of Sciences. – 1992. – V. 323. – No.3. – P. 410 – 414. [in Russian]
- Imanaliev M.I. K teorii pochti solitonnyh reshenij nelinejnogo differencial’nogo uravnenija v chastnyh proizvodnyh tipa Kortevega-de Friza chetvertogo porjadka [To the theory of almost soliton solutions of a nonlinear partial differential equation of the fourth-order Korteweg-de Vries type] / M.I. Imanaliev, T.M. Imanaliev, U.M. Imanaliev // Investigations on integral-differential equations. – Bishkek: Ilim, 2003. – Issue 32. – P.17 – 23. [in Russian]
- Imanaliev M.I. K teorii nelinejnyh uravnenij s differencial’nym operatorom tipa polnoj proizvodnoj po vremeni [On the theory of nonlinear equations with a differential operator of the type of the total time derivative] / M.I. Imanaliev, S.N. Alekseenko // Reports of the Russian Academy of Sciences. – 1993. – V. 329. – No.5. – P. 543 – 546. [in Russian]
- Imanaliev M.I. K teorii nelinejnyh differencial’nyh uravnenij v chastnyh proizvodnyh tipa Kortevega – de Friza [On the theory of nonlinear partial differential equations of the Korteweg-de Vries type] / M.I. Imanaliev, P.S. Pankov, T.M. Imanaliev // Reports of the Russian Academy of Sciences. – 1995. – V. 342. – No. 1. – P.17 – 19. [in Russian]
- Pankov P.S. Priblizhennoe reshenie nachal’noj zadachi dlja nelinejnyh differencial’nyh uravnenij v chastnyh proizvodnyh metodom dopolnitel’nogo argumenta [Approximate solution of the initial value problem for nonlinear partial differential equations by the method of an additional argument] / P.S.Pankov, T.M. Imanaliev, G.M. Kenenbaeva // Anniversary scientific conference dedicated to the 50th anniversary of the development of mathematics in the Academy of Sciences of Kazakhstan: Abstract, reports. – Almaty, 1995. – P. 164. [in Russian]
- Ashirbaeva A.Zh. Reshenie nelinejnyh differencial’nyh i integro-differencial’nyh uravnenij v chastnyh proizvodnyh vysokogo porjadka metodom dopolnitel’nogo argumenta [Solution of nonlinear differential and integral-differential partial differential equations of high order by the method of an additional argument]. – Bishkek: Ilim, 2013. – 134 p. [in Russian]
- Imanaliev M.I. K teorii sistem nelinejnyh integro-differencial’nyh uravnenij v chastnyh proizvodnyh tipa Uizema [On the theory of systems of nonlinear integral-differential partial differential equations of Whitham type] / M.I. Imanaliev, S.N. Alekseenko // Reports of the Academy of Sciences. – 1992. – V. 325. – No. 6. – P.1111 – 1115. [in Russian]
- Ashirbaeva A.Zh. Solution of system of nonlinear differential equations in private first order with multiple variables/ Zh., Ashirbaeva, Zh.I. Mambetov// International research journal. – 2018.– No. 3(69). – P.6-10. [in Russian]






