ДВИЖЕНИЕ В ВЯЗКОЙ СРЕДЕ. ВИДЫ СИЛ СОПРОТИВЛЕНИЯ. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ | Опубликовать статью ВАК, elibrary (НЭБ)

ДВИЖЕНИЕ В ВЯЗКОЙ СРЕДЕ. ВИДЫ СИЛ СОПРОТИВЛЕНИЯ. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ

Научная статья

Волкова А.Ю.¹*, Суетин В.П.²

^{1, 2} Уральский государственный университет путей сообщения, Екатеринбург, Россия

* Корреспондирующий автор (alenavolkova98[at]yandex.ru)

Аннотация

Изучен процесс торможения вращающегося твердого тела. Выполнен модельный эксперимент, в котором трение в системе меняется с помощью парусов, ориентированных под разными углами относительно воздушного потока. Определен интервал скоростей, при которых играют роль различные виды трения: сухое, вязкое и аэродинамическое, а также вычислены основные параметры разных видов трения (момент силы сухого трения, коэффициент вязкого трения), закономерности их изменения в зависимости  от  условий эксперимента.

Ключевые слова: коэффициент сопротивления, вязкое трение, эксперимент

MOVEMENT IN VISCOUS MEDIA. TYPES OF RESISTANCE FORCES. DETERMINATION OF RESISTANCE COEFFICIENTS

Research article

Volkova A.Yu.¹*, Suetin V.P.²

^{1, 2} Ural State University of Railway Transport, Yekaterinburg, Russia

* Correspondent author (alenavolkova98[at]yandex.ru)

Abstract

The process of friction of a rotating solid is studied. A model experiment is performed in which friction in the system is changed using sails oriented at different angles with respect to the airflow. The speed range is determined at which various types of friction play an important role: dry, viscous and aerodynamic, and the main parameters of different types of friction (the moment of dry friction force, coefficient of viscous friction) and the laws of their change depending on the experimental conditions are calculated.

Keywords: resistance factor, viscous friction, experiment.

В процессе торможения любого движущегося тела при разных скоростях играют роли разные виды трения. При самых низких скоростях это сухое трение, когда коэффициент трения не зависит от скорости. Для более высоких скоростей трение будет вязким, когда сила трения зависит от скорости. Далее при еще более высоких скоростях трение уже будет аэродинамическим, когда сила трения пропорциональна квадрату скорости, и так далее. Для исследования видов сил сопротивления мы изучили процесс торможения  вращающегося твердого тела. При этом мы определили интервал скоростей, при которых в процессе торможения  основную  роль играют различные силы торможения (сухое, вязкое, аэродинамическое). Для изменения вязкого и аэродинамического трения на твердое тело устанавливаем два паруса. Изменяя положение парусов относительно потока воздуха, моделируем величину коэффициентов вязкого и аэродинамического трения. Для определения вида трения и коэффициента трения исследуем зависимости угловой скорости вращения тела от времени от времени.

Зависимость угловой скорости вращения твердого тела можно  найти из уравнения динамики вращательного движения [1, с. 140]:

     (1)

где I –  момент инерции системы, М – момент сил сопротивления.

Для сухого трения сила трения не зависит от скорости вращения, а момент силы М = –М₀ = const. В этом случае из уравнения (1) находим:

      (2)

Тогда угловая скорость вращения уменьшается по линейному закону в зависимости от времени.

Вязкое трение характеризуется линейной зависимостью силы трения от скорости движения  (F = αv, где α – коэффициент сопротивления). Зависимость между   моментом   сил   трения и  угловой  скоростью  тоже  будет  линейной (М = –kω) [2, с. 332].

В данном случае решением уравнений (1) и (2) будут следующие зависимости:

       (3)

где γ = k/I. Тогда линейная зависимость угловой скорости от угла поворота системы и зависимость логарифма скорости от времени [3, с. 48]:

      (4)

Если расстояние от оси вращения до каждого из парусов равно R, то коэффициент сопротивления:

       (5)

Коэффициент γ определяется методом наименьших квадратов по зависимости  lnω от времени[4, с. 105].

Для изучения видов сил сопротивления и определения коэффициентов сопротивления собираем схему экспериментальной установки, которая состоит из вращающегося столика, стержня и двух парусов (см. рисунок 1).

 

Рис. 1 – Схема экспериментальной установки

 

Наша установка позволяет определять период вращения от начала вращения вплоть до остановки тела. Для определения средней угловой скорости вращения при прохождении n-ого оборота воспользуемся ее определением
[5, с. 13]:

        (6)

Так как угловая скорость является переменной величиной, то полученное ее значение является средним значением угловой скорости за n-й период вращения [6, с. 113].

Определение видов сил сопротивления и определение коэффициентов сопротивления

На рис. 2 представлен экспериментальный график зависимости угловой скорости вращения столика от времени для ориентации парусов вдоль потока (φ=0⁰).

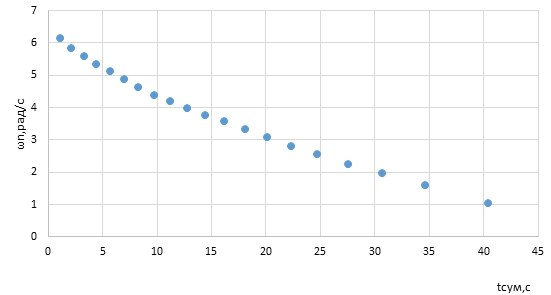
Рис. 2 – График зависимости угловой скорости вращения столика от времени для угла ориентации парусов
вдоль воздушного потока (φ=0⁰)

 

График нелинейный, по нему трудно отделить интервалы времени в которых преобладают определенные виды трения. По полученным расчетам также построим график зависимости логарифма угловой скорости вращения столика от времени для угла ориентации парусов для 0⁰. По графику видно, что наблюдается излом зависимости, если  интервал времени  примерно 20 секунд. Значит мы наблюдаем границу разных видов трения. Если время меньше 20 секунд трение будет вязким график в этом диапазоне линейный, если же интервал времени больше 20 секунд, то трение будет сухое, тангенс угла наклона зависимости в этой точке изменяется. При данных скоростях вращения  участок интервалов времени, в котором трение считается аэродинамическим, обнаруживается только  на двух начальных точках.

 

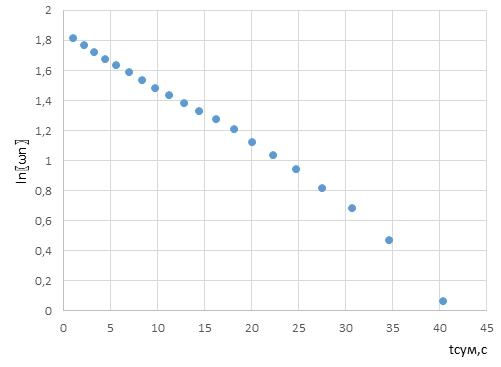
Рис. 3 – График зависимости логарифма угловой скорости вращения столика от времени
для угла ориентации парусов 0⁰

 

Аналогично были построены графики и выделены области разных видов трения для углов ориентации парусов 30⁰, 60⁰ и 90⁰. Для всех зависимостей методом наименьших квадратов были определены тангенсы углов наклона зависимостей угловой скорости от времени для сухого трения и логарифма угловой скорости от времени для вязкого. Переход с одного вида трения на другое наблюдается при угловой скорости вращения 1 рад/с.

Таким образом, с помощью метода наименьших квадратов по зависимости угловой скорости вращения столика от времени, мы определили отношение момента силы трения к моменту инерции для сухого трения.

Вычислили момент силы сухого трения М_тр по формуле [7, с. 61]:

     (7)

где β – это отношение момента силы трения к моменту инерции для сухого трения, а I – момент инерции системы, который определяется отдельно. Момент силы сухого трения слабо зависит от угла ориентации парусов [8, с. 132]. Среднее его значение указано в Таблице 1.

Также с помощью метода наименьших квадратов по зависимости логарифма угловой скорости вращения столика от времени для вязкого трения, мы определили коэффициент γ.

После чего вычислили коэффициент вязкого трения по формуле [9, с. 29]:

      (8)

где γ – коэффициент, определенный с помощью метода наименьших квадратов по зависимости логарифма угловой скорости вращения столика от времени для вязкого трения, R – расстояние от оси вращения до каждого из парусов (R = 0,13 м) [10, с. 31]. Результаты измерений и вычислений момента силы сухого трения и коэффициента вязкого трения заносим в Таблицу 1.

 

Таблица 1 – Результаты измерений и вычислений момента силы сухого трения и коэффициента вязкого трения
от угла ориентации парусов относительно воздушного потока

Угол ориентации парусов φ, град.	Отношение момента силы трения к моменту инерции для сухого трения  β, 1/с	Момент силы сухого трения , Н∙м	Коэффициент γ, 1/с	Коэффициент вязкого трения α, кг/с
0	0,14	0,001	0,0362	0,007358
30			0,0912	0,018537
60			0,1152	0,023415
90			0,1413	0,02872

По полученным результатам для коэффициента вязкого трения построим график зависимости коэффициента вязкого трения от угла поворота парусов (см. рис. 4).

 

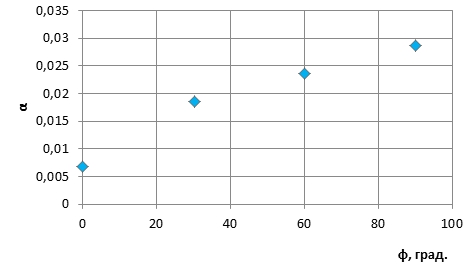
Рис. 4 – Зависимость коэффициента вязкого трения от угла ориентации парусов

 

График зависимости коэффициента вязкого трения от угла поворота парусов нелинейный. При изменении угла поворота парусов относительно воздушного потока коэффициент вязкого трения увеличивается в 4 раза.

Данное исследование  иллюстрирует экспериментальное доказательство существования различных  видов трения, позволяет определить их границы по величине скорости вращения, а также позволяет определить важнейшие параметры  сил трения и их зависимость  от внешних условий эксперимента.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

 

Список литературы / References

1. Савельев И.В. Курс общей физики, главная редакция физико-математической литературы. В 3 т. Т. 1 Механика, колебания и волны, молекулярная физика / И.В. Савельев. – М.: Наука, 1970. – 511 с.
2. Матвеев А.Н. Механика и теория относительности. 3-е изд. / А.Н. Матвеев. – М.: ОНИКС 21 век: Мир и Образование, 2003. — 432 с.
3. Иродов И.Е. Курс общей физики. В 5 т. Т. 1 Механика. Основные законы / И.Е. Иродов. – М.: 2010. — 309 с.
4. Сивухин Д.В. Общий курс физики. В 5 т. Т. 1 Механика / Д.В. Сивухин. – М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. – 560 с.
5. Трофимов Т.И. Курс физики. 11-е изд. / Т.И. Трофимов. – М.: 2006.— 560 с.
6. Джанколи Д. Физика. В 2 т. Т. 1 Механика / Д. Джанколи. – М.: Мир; 1989 – 656 с.
7. Детлаф А.А., Яворский Б.М. Курс физики / А.А. Детлаф., Б.М. Яворский. – М.: Высш. шк. , 2002. – 718 с.
8. Ландсберг Г.С.Элементарный учебник физики. В 3 т. Т.1 Механика. Теплота. Молекулярная физика / Г.С. Ландсберг. – Том 1: 2010 – 612с.
9. Суетин В.П. Механика / В.П. Суетин., Д.В. Суетин, В.Е. Макаров // Методические указания к выполнению лабораторных работ по физике для студентов всех форм обучения: УрГУПС, Екатеринбург. – 2011 . – 72 с.
10. Светозаров В.В. Лабораторный комплекс ЛКМ-1, Механика / В.В. Светозаров // Научно-технический центр Владис, Москва. – 2000. – 56 с.

Список литературы на английском языке / References in English

1. Savelev I.V. Kurs obshhej fiziki, glavnaja redakcija fiziko-matematicheskoj literatury. V 3 t. T. 1 Mehanika, kolebanija i volny, molekuljarnaja fizika [General physics course, the main edition of the physical and mathematical literature. V. 1 Mechanics, vibrations and waves, molecular physics] / I.V. Savel’ev. – M.: Nauka, 1970. – 511 p. [in Russian]
2. Matveev A.N. Mehanika i teorija otnositel’nosti.[Mechanics and theory of relativit 3rd ed] ./ A.N. Matveev. – M.: ONIKS 21 vek: Mir i Obrazovanie, 2003. – 432 p. [in Russian]
3. Irodov I.E. Kurs obshhej fiziki. V 5 t. T. 1. Mehanika. Osnovnye zakony [General physics course. In 5 vols. V. 1 Mechanics. Basic laws] / I.E. Irodov. – M.: 2010. — 309 p. [in Russian]
4. Sivuhin D.V. Obshhij kurs fiziki. V 5 t. T. 1 Mehanika [General physics course. In 5 vols. V. 1 Mechanics] / D.V. Sivuhin. – M.: FIZMATLIT; Izd-vo MFTI, 2005. – 560 p. [in Russian]
5. Trofimov T.I. Kurs fiziki. 11-th ed. [Physics course] / T.I. Trofimov. – M.: 2006.— 560 p. [in Russian]
6. Dzhankoli D. Fizika. V 2 t. T. 1 Mehanika [Physics. In 2 vols. V. 1 Mechanics] / D. Dzhankoli. – : Mir; 1989 – 656 p. [in Russian]
7. Detlaf A.A., Javorskij B.M. Kurs fiziki [Physics Course] / A.A. Detlaf., B.M. Javorskij. – : Vyssh. shk. , 2002. – 718 p. [in Russian]
8. Landsberg G.S.Jelementarnyj uchebnik fiziki. V 3 t. T.1 Mehanika. Teplota. Molekuljarnaja fizika [Elementary textbook of physics. In 3 vols. V.1 Mechanics. Heat. Molecular Physics] / G.S. Landsberg. – Tom 1: 2010 – 612 p. [in Russian]
9. Suetin V.P. Mehanika [Mechanics] / V.P. Suetin., D.V. Suetin, V.E. Makarov // Metodicheskie ukazanija k vypolneniju laboratornyh rabot po fizike dlja studentov vseh form obuchenija [Methodological instructions for the implementation of laboratory work in physics for students of all forms of education]: UrGUPS, Ekaterinburg. – 2011 . – 72 p. [in Russian]
10. Svetozarov V.V. Laboratornyj kompleks LKM-1, Mehanika [Laboratory complex LKM-1, Mechanics] / V.V. Svetozarov // Nauchno-tehnicheskij centr Vladis, Moskva. – 2000. – 56 p. [in Russian]