ОЦЕНКА ВТОРЫХ ПРОИЗВОДНЫХ ЯКОБИАНА ДЛЯ СЛОЖНОЙ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ И ИХ ВЛИЯНИЯ НА СТАТИЧЕСКУЮ УСТОЙЧИВОСТЬ | Опубликовать статью ВАК, elibrary (НЭБ)

ОЦЕНКА ВТОРЫХ ПРОИЗВОДНЫХ ЯКОБИАНА ДЛЯ СЛОЖНОЙ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ И ИХ ВЛИЯНИЯ НА СТАТИЧЕСКУЮ УСТОЙЧИВОСТЬ

Научная статья

Зуев А.И.^1, *, Аверьянов Д.А.², Антаненков А.А.³, Булатов Р.В.⁴, Бурмейстер М.В.⁵

¹ ORCID: 0000-0002-1853-3222;

² ORCID: 0000-0002-0836-3135;

⁵ ORCID: 0000-0002-8787-7299;

^{1, 2, 3, 4} НИУ «МЭИ», Москва, Россия;

⁵ Научно-технический Центр Федеральной сетевой компании Единой энергетической системы, Москва, Россия

* Корреспондирующий автор (zuyevali[at]mpei.ru)

Аннотация

Исследована оценка вторых производных определителя матрицы Якоби (якобиана) уравнений установившегося режима для сложной электроэнергетической системы, а также произведен анализ их влияния на апериодическую составляющую статической устойчивости энергосистем. Создан автоматизированный алгоритм по вычислению якобиана, также его первых и вторых производных. Показано применение алгоритма на тестовой схеме IEEE-14 для нахождения предельного режима по статической апериодической устойчивости с использованием результатов расчета последовательного утяжеления всех нагрузочных узлов схемы.

Ключевые слова: предельный режим, статическая апериодическая устойчивость, установившийся режим, электроэнергетическая система, якобиан, первые и вторые производные якобиана.

ESTIMATION OF THE SECOND JACOBIAN DERIVATIVES FOR A COMPLEX ELECTRIC POWER SYSTEM AND THEIR INFLUENCE ON STATIC STABILITY

Research article

Zuev A.I.^1, *, Averyanov D.A. ², Antanenkov A.A. ³, Bulatov R.V. ⁴, Burmeister M.V.⁵

¹ ORCID: 0000-0002-1853-3222;

² ORCID: 0000-0002-0836-3135;

⁵ ORCID: 0000-0002-8787-7299;

^{1, 2, 3, 4} NRU “MEI”, Moscow, Russia;

⁵ Scientific and Technical Centre of the Federal Network Company of the Unified energy system, Moscow, Russia

* Corresponding author (zuyevali[at]mpei.ru)

Abstract

In this article, the authors study the estimation of the second derivatives of the determinant of the Jacobi matrix (Jacobian) of steady-state equations for a complex electric power system and analyze their influence on the aperiodic component of the static stability of power systems. An automated algorithm for calculating the Jacobian, as well as its first and second derivatives, has been created. The application of the algorithm is shown on the test scheme IEEE-14 for finding the limit mode for static aperiodic stability using the results of calculating the sequential weighting of all load nodes of the scheme.

Keywords: limit mode, static aperiodic stability, steady-state mode, electric power system, Jacobian, the first and the second derivatives of the Jacobian.

Введение

В настоящее время проблема поиска области существующих режимов (ОСР) по статической апериодической устойчивости сохраняется. Задача исследования заключается в упрощении поиска ОСР на основе результатов расчета утяжеления нагрузочных узлов и значений контролируемых величин. Это позволит ускорить и упростить работу диспетчеров на подстанциях при оперативном планировании и ведении режима.

Выпущено большое количество научных трудов по использованию якобиана, а также информации о его вторых производных в качестве показателя по оценке статической апериодической устойчивости. Впервые в учебном пособии [1] было описано применение вторых производных якобиана для исследования сходимости метода Ньютона при расчете установившегося режима (УР) энергосистемы. Однако не было предложено компьютеризированного алгоритма, который использовал бы интересующую информацию о якобиане и его вторых производных для оценки апериодической устойчивости. Позднее, в задачнике [2] расчеты УР и последующая оценка апериодической устойчивости ведутся лишь по оценке знака якобиана без использования информации о его вторых производных, что является неполным анализом апериодической устойчивости. В диссертации [3] введено понятие «обобщённые показатели» для оценки апериодической устойчивости. В качестве них автором были взяты вторые производные потерь активной мощности и вторые производные якобиана. В работе был разработан компьютеризированный алгоритм с использованием данных обобщенных показателей, который был успешно апробирован на диспетчерских пунктах Амурской энергосистемы. Однако с течением времени, данный алгоритм устарел, в связи с чем появляется необходимость обновления программного обеспечения (ПО). Обзор зарубежных монографий [4], [7], [8] по рассматриваемой теме показал, что исследования с использованием информации о якобиане энергосистемы ведутся до сих пор, но работ с использованием вторых производных не было найдено, что подтверждает актуальность данного исследования.

Формирование алгоритма

В работе [3] уже было рассмотрено влияние обобщенных параметров на задачи управления установившегося режима, в том числе якобиана, его первых и вторых производных. Автор рассматривает влияние этих величин для случая простейшей системы «генератор – шины бесконечной мощности» при утяжелении нагрузки. В результате расчета были получены следующие характеристики (рисунок 1).

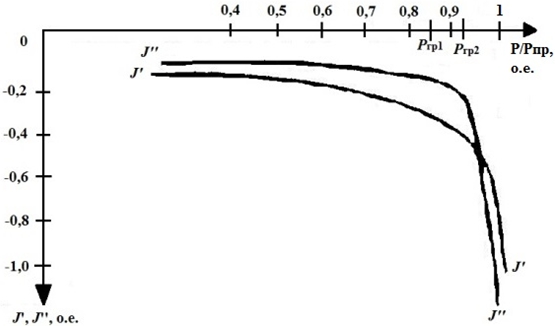
Рис. 1 – Зависимость первых J‘ и вторых производных якобиана J” при утяжелении нагрузки
для случая простейшей схемы «генератор – шины бесконечной мощности»

 

Из данного графика можно сделать следующие выводы [3]: при увеличении мощности нагрузки P наблюдается незначительное уменьшение значения вторых производных якобиана J“. Однако, при приближении к области предельных режимов даже небольшое увеличение P приводит к значительному увеличению J“. Таким образом, такое распределение нагрузок, а соответственно и УР, при котором  является претендентом на существование предельного режима по апериодической статической устойчивости. В этом случае принимается, что УР, рассчитанный на i-ой итерации, является предельным режимом по апериодической статической устойчивости. Граничная точка между областями с незначительным и интенсивным увеличением второй производной якобиана по модулю может служить характеристикой, определяющей приближение режима к области существующих режимов, что наглядно продемонстрировано в рамках данной исследовательской работы.

Также следует упомянуть о том, что внутри заведомо устойчивых режимов значение якобиана J имеет выпуклость сверху, поскольку в этом случае J“ < 0. По концам рассматриваемого интервала утяжеления J“ → ‒ ∞, при этом J имеет точки перегиба в виде выпуклости при приближении к ОСР.

Ниже представлен план разработки алгоритма для оценки якобиана и его вторых производных при утяжелении нагрузочных узлов.

Алгоритм выполнения этой задачи выглядит следующим образом [9]:

1. Загрузка исходных данных в RastrWin3 и их вывод в отчёт, обработка исходных данных, подготовка к расчёту.

Исходные данные загружаются в программно-вычислительный комплекс (ПВК) RastrWin3 либо в формате .rg2, либо импортируются из других форматов, например, – .cdu. Поэтому для корректной работы алгоритма параметры схемы необходимо представить именно в таком виде.

2. Расчет режима при представлении нагрузки постоянным отбором мощности и вывод значения якобиана, рассчитанного на каждой итерации. в отчёт.

Перед расчётом режима в ПВК RastrWin3 необходимо задать все нагрузки и генерацию исходной схемы. Для этого в алгоритме применяется встроенная утилита RastrWin3 под названием «групповая коррекция» [10].

При расчётах рабочих режимов электрических сетей нагрузка обычно характеризуется неизменными активной и реактивной мощностями P, Q = const. Такое представление нагрузки соответствует замене действительных характеристик нагрузки условными. Эти изменения обычно соответствуют условиям, принимаемым при проектных расчетах электрических сетей [2, 11] и приемлемо при расчетах УР.

3. Поочередное утяжеление каждого нагрузочного узла схемы, вывод результатов утяжеления в файл.

Утяжеление реализовано в виде цикла, на каждом шаге которого производится расчет установившегося режима. По результатам каждого шага цикла утяжеления в отчет выводятся контролируемые величины.

Согласно методическим указаниям по расчёту устойчивости энергосистем [12], критерием достижения предельного режима является расхождение расчёта режима или снижение напряжения менее чем на 0,7U_ном. Также в качестве дополнительного критерия окончания расчетов утяжеления принимается превышение количества максимальных итераций на шаге расчёта, равных десяти, так как среднее количество итераций при расчётах УР в ПВК.

По результатам расчёта в i-ом узле при достижении предельного режима производится возврат исходных значений нагрузок во всех нагрузочных узлах для дальнейшего расчёта утяжеления в (i+1)-ом узле.

В отчет выводятся значения якобиана J для каждого значения нагрузки в узле. По полученным значениям якобиана далее производится расчёт J‘ и J“ и построение необходимых графиков.

Расчет первых и вторых производных якобиана нагляднее можно проиллюстрировать с помощью примера. Пусть в результате расчета утяжеления режима для абстрактного узла 1 были получены следующие значения:

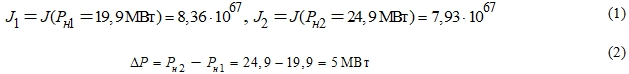
Тогда первые и вторые производные якобиана приближенно будут определяться следующим образом:

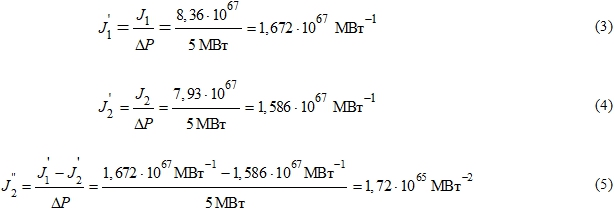
4. Извещение о завершении расчёта в окне консоли RastrWin3.

Для того чтобы пользователь смог отслеживать процесс работы алгоритма, после каждого выполненного пункта в окне консоли выдается сообщение об удачном завершении этапа расчета.

5. Оформление отчета в Microsoft Excel, построение необходимых графиков.

Задача алгоритма для Microsoft Excel состоит в расчёте J‘ и J“ и построении графиков J (П) и J“ (П), а также придании лаконичного и наглядного вида результатам расчёта. Для каждого нагрузочного узла должны быть получены 2 графика.

На рисунке 2 представлена блок-схема разрабатываемого алгоритма.

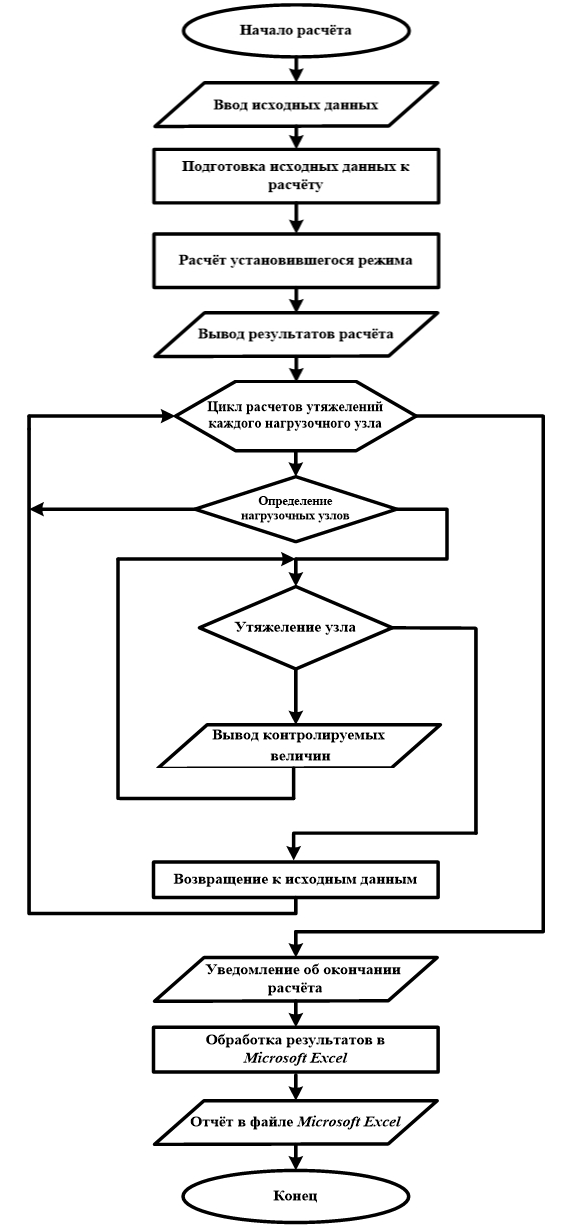
Рис. 2 – Блок-схема разрабатываемого алгоритма

 

Апробация алгоритма на тестовой схеме IEEE-14

В качестве проверки работоспособности созданного алгоритма необходимо апробировать его на тестовой схеме. Тестовые схемы – это ряд стандартных схем различных электрических сетей, составленный в ходе получения опыта эксплуатации и управления в электроэнергетике, используемый для решения научных и инженерных задач, таких как: расчеты УР, моделирование переходных процессов, расчеты надежности электроснабжения, оптимизация режимов энергосистем и др. В общем случае позволяют протестировать предлагаемые решения на схемах близких к реальным и обеспечить повторяемость результатов исследований. В качестве тестовой схемы выбрана схема IEEE-14 (рисунок 3) [13]. Схема отображает часть среднезападной системы США от февраля 1962 года и была составлена в качестве испытательной в 1993 году. Схема включает в себя 14 узлов, из которых в 5 узлах действуют синхронные машины и в 11 сконцентрированы потребители электроэнергии.

Рис. 3 – Тестовая схема IEEE-14 [9]

 

В таблице 1 представлены исходные данные для узлов схемы, а в таблице 2 – по ветвям [14].

 

Таблица 1 – Исходные данные по узлам схемы IEEE-14

Узел	Тип	Uном, кВ	Bш, мСм	Напряжение		Pн, МВт	Qн, Мвар	Pг, МВт	Qг, Мвар	Qmin, Мвар	Qmax, Мвар
				U, кВ	φ, град
1	База	230	–	243,8	0	–	–	232,3	-16,8	–	–
2	Ген	230	–	240,35	-4,983	21,7	12,7	40	43,446	-40	50
3	Ген	230	–	232,3	-12,725	94,2	19	0,001	25,022	–	40
4	Нагр	230	–	234,064	-10,313	47,8	-3,9	–	–	–	–
5	Нагр	230	–	234,488	-8,774	7,6	1,6	–	–	–	–
6	Ген	115	–	123,050	-14,221	11,2	7,5	0,001	12,737	-6	24
7	Нагр	115	–	122,075	-13,36	–	–	–	–	–	–
8	Ген	115	–	125,35	-13,36	–	–	0,001	17,664	-6	24
9	Нагр	115	1,4367	121,432	-14,939	29,5	16,6	–	–	–	–
10	Нагр	115	–	120,483	-15,097	9	5,8	–	–	–	–
11	Нагр	115	–	121,544	-14,791	3,5	1,8	–	–	–	–
12	Нагр	115	–	121,347	-15,076	6,1	1,6	–	–	–	–
13	Нагр	115	–	120,794	-15,156	13,5	5,8	–	–	–	–
14	Нагр	115	–	119,086	-16,034	14,9	5	–	–	–	–

 

Таблица 2 – Исходные данные по ветвям схемы IEEE-14

№ нач.	№ кон.	R, Ом	X, Ом	Bш, мСм	kтр
1	2	10,2520	31,3010	0,0998	–
1	5	28,5819	117,9882	0,0993	–
2	3	24,8577	104,7261	0,0828	–
2	4	30,7402	93,2733	0,0643	–
2	5	30,1266	91,9825	0,0654	–
3	4	35,4483	90,4749	0,0242	–
4	5	7,0622	22,2762	–	–
4	7	0,0001	105,8105	–	0,511
4	9	0,0001	276,2604	–	0,516
5	6	0,0001	115,8037	–	0,536
6	11	12,5611	26,3045	–	–
6	12	16,2548	33,8309	–	–
6	13	8,7483	17,2282	–	–

 

Окончание таблицы 2 – Исходные данные по ветвям схемы IEEE-14

№ нач.	№ кон.	R, Ом	X, Ом	Bш, мСм	kтр
7	8	0,0001	23,2958	–	–
7	9	0,0001	14,5488	–	–
9	10	4,2069	11,1751	–	–
9	14	16,8103	35,7578	–	–
10	11	10,8511	25,4013	–	–
12	13	29,2167	26,4341	–	–
13	14	22,6055	46,0256	–	–

 

Параметры данной схемы перенесены в соответствующие графы таблиц «Узлы» и «Ветви» в ПВК RastrWin3.

Результаты расчета УР для схемы IEEE-14 с использованием алгоритма приведены в таблицах 3 – 4.

 

Таблица 3 – Результаты расчёта УР для схемы IEEE-14. Данные по узлам

Номер узла	Название узла	Pнагр, МВт	Qнагр, Мвар	Pген, МВт	Qген, Мвар	Uузл, кВ	Фаза, град
1	Узел 1	0	0	232,383	-16,777	243,8	0
2	Узел 2	21,7	12,7	40	43,446	240,35	-0,087
3	Узел 3 (СК)	94,2	19	0,001	25,022	232,3	-0,222
4	Узел 4	47,8	-3,9	0	0	234,085	-0,180
5	Узел 5	7,6	1,6	0	0	234,510	-0,153
6	Узел 6 (СК)	11,2	7,5	0,001	12,737	123,05	-0,248
7	Узел 7	0	0	0	0	122,067	-0,233
8	Узел 8 (СК)	0	0	0,001	17,664	125,35	-0,233
9	Узел 9	29,5	16,6	0	0	121,416	-0,261
10	Узел 10	9	5,8	0	0	120,850	-0,263
11	Узел 11	3,5	1,8	0	0	121,538	-0,258
12	Узел 12	6,1	1,6	0	0	121,345	-0,263
13	Узел 13	13,5	5,8	0	0	120,792	-0,265
14	Узел 14	14,9	5	0	0	119,076	-0,280

 

Таблица 4 – Результаты расчёта УР для схемы IEEE-14. Данные по ветвям

№ нач.	№ кон.	Sнач, МВ·А	Sкон, МВ·А	ΔP, МВт	ΔQ, Мвар
1	2	156,9-j20,4	152,6-j27,7	4,297	13,119
1	5	75,5+j3,6	72,8-j2,1	2,763	11,405
2	3	73,2+j3,6	70,9-j1,6	2,323	9,786
2	4	56,1-j1,6	54,5-j3,1	1,677	5,087
2	5	41,5+j1,1	40,6+j2	0,904	2,759
3	4	23,3-j4,4	23,7-j4,8	0,373	0,953
4	5	61,2-j15,8	61,7-j14,2	0,514	1,622
4	7	28,1-j9,6	28,1-j11,3	0	1,699
4	9	16,1-j0,4	16,1-j1,7	0	1,303
5	6	44,1+j12,5	44,1+j8,1	0	4,424
6	11	7,4+j3,6	7,3+j3,5	0,056	0,116
6	12	7,8+j2,5	7,7+j2,4	0,072	0,150
6	13	17,7+j7,2	17,5+j6,8	0,212	0,418
7	8	+j17,2	+j17,7	0	0,463
7	9	28,1+j5,8	28,1+j5	0	0,802
9	10	5,2+j4,2	5,2+j4,2	0,013	0,034
9	14	9,4+j3,6	9,3+j3,3	0,116	0,247
10	11	3,8+j1,6	3,8+j1,7	0,013	0,030
12	13	1,6+j0,8	1,6+j0,8	0,006	0,006
13	14	5,6+j1,8	5,6+j1,7	0,054	0,110

 

В качестве доказательства исправности работы написанного алгоритма представлено утяжеление узлов 12 (табл. 5 и рис. 4) и 13 (табл. 6 и рис. 5) тестовой схемы, а также проведен анализ полученных результатов.

 

Таблица 5 – Результаты расчёта утяжеления для узла 12

Pн, МВт	U, кВ	Фаза, град	Sнач, МВ·А	Sкон, МВ·А	ΔP, МВт	J	J‘	J”
11	120,836	-0,281	10,7+j3	10,6+j2,7	13,988	8,537E+67	1,707E+67	1,023E+65
16	120,314	-0,299	13,7+j3,6	13,4+j3,1	14,653	8,281E+67	1,656E+67	1,045E+65
21	119,783	-0,317	16,6+j4,1	16,3+j3,5	15,390	8,020E+67	1,604E+67	1,064E+65
26	119,240	-0,335	19,6+j4,8	19,2+j3,9	16,200	7,754E+67	1,551E+67	-9,367E+69
31	118,686	-0,354	22,6+j5,5	22+j4,3	17,086	2,342E+71	4,685E+70	4,104E+68
36	118,120	-0,373	25,6+j6,2	24,9+j4,7	18,051	2,240E+71	4,480E+70	-4,103E+72
41	117,043	-0,393	28,7+j6,9	27,7+j5	19,122	1,028E+74	2,056E+73	6,837E+71
46	115,833	-0,413	31,7+j7,7	30,6+j5,3	20,300	8,572E+73	1,714E+73	6,151E+71
51	114,550	-0,435	34,8+j8,6	33,4+j5,6	21,591	7,034E+73	1,407E+73	5,460E+71

 

Окончание таблицы 5 – Результаты расчёта утяжеления для узла 12

Pн, МВт	U, кВ	Фаза, град	Sнач, МВ·А	Sкон, МВ·А	ΔP, МВт	J	J‘	J”
56	113,183	-0,456	37,9+j9,5	36,2+j5,9	23,006	5,669E+73	1,134E+73	4,773E+71
61	111,723	-0,479	41,1+j10,5	39+j6,3	24,560	4,476E+73	8,952E+72	-2,295E+77
66	109,674	-0,505	44,3+j11,7	41,9+j6,6	26,368	5,739E+78	1,148E+78	1,028E+77
71	107,267	-0,534	47,6+j12,9	44,7+j6,9	28,434	3,168E+78	6,337E+77	6,348E+76
76	104,542	-0,566	50,9+j14,4	47,5+j7,2	30,819	1,581E+78	3,163E+77	3,596E+76
81	101,375	-0,602	54,4+j16,1	50,3+j7,6	33,635	6,824E+77	1,365E+77	1,792E+76
86	97,547	-0,644	57,9+j18,1	53+j7,9	37,084	2,344E+77	4,689E+76	–
Режим разошёлся

 

 

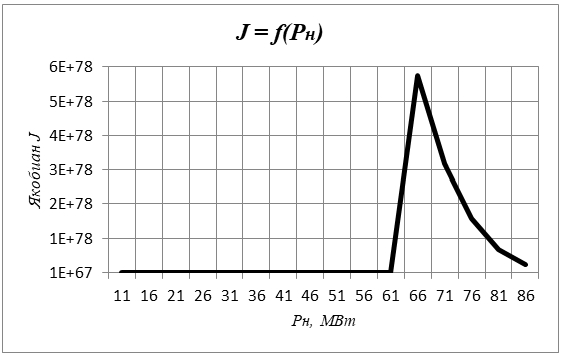
Рис. 4 – График J (P_н) для узла 12

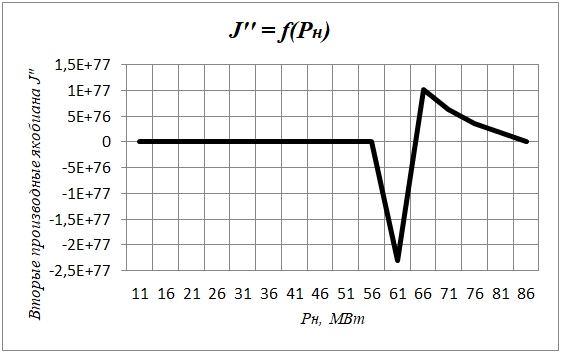
Рис. 5 – График J“ (P_н) для узла 12

 

По представленным таблицам и зависимостям видно, что наблюдается увеличение значений J” по модулю на 5 порядков при приближении к P_н = 26 МВт затем их снижение на порядок при P_н = (26 ÷ 31) МВт. После происходит увеличение значений J” по модулю на 4 порядка и их постепенное снижение при P_н = (36 ÷ 56) МВт. Однако, начиная с P_н = 61 МВт, наблюдается резкое увеличение J” по модулю сразу на 6 порядков, а затем их постепенное снижение. Таким образом, можно сделать вывод о том, что при достижении P_н = 61 МВт, ЭЭС находится в околопредельном режиме по статической апериодической устойчивости [3].

Экстремумы, получаемые при построении зависимостей, свидетельствуют о том, что при достижении P_н = 61 МВт ЭЭС выходит на верхний предел по реактивной мощности в генераторных узлах Q_max. В этом случае в ПВК RastrWin3 используется модель генератора P_г , Q_г = const при наступлении ограничения по реактивной мощности с одновременным расчетом якобиана по установившейся форме, то есть при моделировании P_г , U_г = const.

 

Таблица 6 – Результаты расчета утяжеления для узла 13

Pн, МВт	U, кВ	Фаза, град	Sнач, МВ·А	Sкон, МВ·А	ΔP, МВт	J	J‘	J”
18	120,527	-0,279	20,9+j7,6	20,6+j7	14,005	8,550E+67	1,710E+67	9,618E+64
23	120,257	-0,294	24+j8	23,6+j7,3	14,663	8,309E+67	1,662E+67	9,728E+64
28	119,982	-0,309	27,2+j8,4	26,7+j7,5	15,365	8,066E+67	1,613E+67	9,821E+64
33	119,704	-0,324	30,3+j8,9	29,8+j7,7	16,112	7,820E+67	1,564E+67	-9,474E+69
38	119,419	-0,340	33,5+j9,4	32,8+j8	16,905	2,369E+71	4,739E+70	3,783E+68
43	119,131	-0,355	36,7+j9,9	35,9+j8,3	17,746	2,275E+71	4,550E+70	3,767E+68
48	118,838	-0,370	39,9+j10,5	39+j8,6	18,636	2,181E+71	4,361E+70	-3,931E+72
53	117,975	-0,387	43,1+j10,8	42+j8,5	19,605	9,850E+73	1,970E+73	5,758E+71
58	117,175	-0,403	46,3+j11,2	44,9+j8,6	20,632	8,410E+73	1,682E+73	5,311E+71
63	116,319	-0,421	49,5+j11,6	48+j8,6	21,730	7,082E+73	1,416E+73	4,691E+71
68	115,430	-0,438	52,7+j12,1	50,9+j8,6	22,897	5,910E+73	1,182E+73	4,155E+71
73	114,493	-0,456	55,9+j12,6	53,9+j8,6	24,140	4,871E+73	9,742E+72	-2,449E+77
78	112,855	-0,477	59,2+j13,3	56,9+j8,8	25,584	6,124E+78	1,225E+78	9,363E+76
83	111,222	-0,498	62,5+j14	60+j8,9	27,131	3,783E+78	7,566E+77	6,257E+76
88	109,446	-0,522	65,9+j14,8	62,9+j8,9	28,831	2,219E+78	4,437E+77	4,008E+76
93	107,490	-0,546	69,3+j15,6	65,9+j9	30,716	1,217E+78	2,434E+77	2,418E+76
98	105,309	-0,573	72,7+j16,6	68,9+j9,1	32,829	6,123E+77	1,225E+77	1,439E+76
103	102,625	-0,605	76,3+j17,7	71,9+j9,1	35,387	2,526E+77	5,051E+76	6,544E+75
108	99,558	-0,641	79,9+j19,1	74,9+j9,2	38,342	8,898E+76	1,780E+76	2,674E+75
113	95,693	-0,684	83,6+j20,7	77,7+j9,2	42,056	2,213E+76	4,426E+75	–
Режим разошёлся

 

 

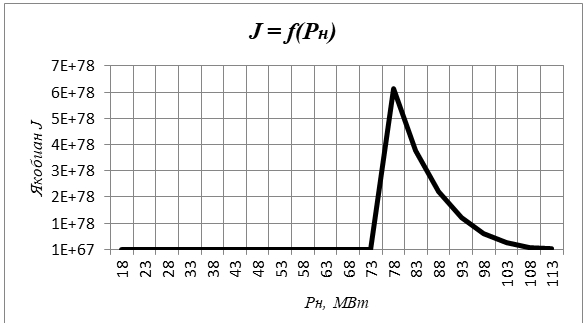
Рис. 6 – График J (P_н) для узла 13

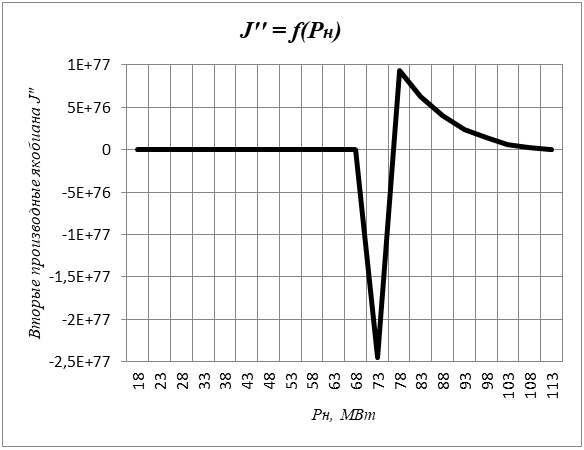
Рис. 7 – Графики J“ (P_н) для узла 13

 

По аналогии с предыдущим анализом установлено, что при достижении P_н = 73 МВт, ЭЭС находится в околопредельном режиме по статической апериодической устойчивости

Результаты

В ходе проведенного исследования был разработан алгоритм для нахождения якобиана, его первых и вторых производных на современном ПВК RastrWin3 с последующей доработкой отчета в Microsoft Excel. Он был апробирован на тестовой схеме энергосистемы, что свидетельствует об адекватности результатов исследования. В ходе проведенного анализа были получены значения околопредельной мощности нагрузки по статической апериодической устойчивости для двух произвольных узлов рассматриваемой энергосистемы.

Заключение

Установлена важность применения таких обобщенных показателей режима, как якобиан, его первые и вторые производные с точки зрения определения границы области допустимых режимов электроэнергетической системы.

Разработан алгоритм для нахождения обобщённых показателей якобиана, его первых и вторых производных, успешно реализованный на современном программно-вычислительном комплексе RastrWin3 с последующей доработкой отчета в Microsoft Excel.

Успешная апробация алгоритма на тестовой схеме IEEE-14 позволила сделать важные выводы касательно рассматриваемых в данной работе обобщенных показателей, а именно:

• при некотором установившемся режиме, который находится достаточно далеко от предела по статической устойчивости, якобиан и его вторые производные меняются достаточно незначительно;
• при приближении к пределу по статической апериодической устойчивости вторые производные якобиана резко возрастают по абсолютной величине;
• краевая точка между областями с незначительным и интенсивным увеличением второй производной якобиана по модулю может служить характеристикой, определяющей приближение режима к области существующих режимов.

Благодарности Авторы выражают искреннюю благодарность д.т.н., проф., Чемборисовой Н.Ш. в подготовке и сопровождении работы по данному исследованию.	Acknowledgement The authors are sincerely grateful to PhD in Engineering, Professor Chemborisova N. Sh. in preparation and maintenance of work on this study.
Конфликт интересов Не указан	Conflict of Interest None declared

Список литературы / References

1. Идельчик В. И. Расчеты установившихся режимов электрических систем, М.: Энергия, 1977. – 192 с.
2. Ежков В. В. Электрические системы и сети в примерах и иллюстрациях / В. В. Ежков, Г. К. Зарудский, Э. Н. Зуев и др. – Москва, Высшая школа, 1999. – 352 с.
3. Чемборисова Н. Ш. Обобщенные показатели в задачах управления установившимися режимами в расчетах электроэнергетических систем, Диссертация на соискание ученой степени доктора технических наук – Иркутск, 2004.
4. Jerosolimski M. A new method for fast calculation of Jacobian matrices: automatic differentiation for power system simulation / Jerosolimski M., Levacher L. // IEEE Transactions on Power Systems, 9(2), pp. 700-706, 1994.
5. Zhang Y. P. Research on the relationship of the singular point for load flow jacobian matrix and the critical point of voltage collapse / Zhang Y, P., Huang W., Liu Z. Q., Yang J. Y., Cai X. L., Zhang J. H. IEEE Power Engineering Society General Meeting, 2005.
6. Naik S. D. On critical mode of bifurcation point and loadability in shunt compensated multi-bus power system / Naik S. D., Khedkar M. K., Bhat S. S. // International Conference on Power and Energy Systems, 2011.
7. Raja Masood Larik A statistical jacobian application for power system optimization of voltage stability / Raja Masood Larik, Mohd,Wazir Mustafa, Manoj Kumar Panjwani, 2019.
8. Yue Songa State-in-mode analysis of the power flow Jacobian for static voltage stability / Yue Songa, David J, Hilla, Tao Liua, 2019.
9. Чемборисова Н. Ш. Использование моделей элементов сети и ПК RASTR WIN при расчетах и анализе режимов ЭЭС: учебное пособие по курсу «Применение ЭВМ в электроэнергетике» по направлению «Электроэнергетика и электротехника» / Н. Ш. Чемборисова, М. В. Бурмейстер, И. Х. Юсупов– М.: Издательство МЭИ, 2018. – 68 с.
10. Нейумин В. Г. Программный комплекс «RastrWin3», Руководство пользователя / В. Г. Нейумин, Е. В. Машалов, А. С. Александров, А. А. Багрянцев. 25.12.2018.
11. Веников В.А. Электрические системы. Математические задачи электроэнергетики: Учебник для студентов вузов – 2-е изд., перераб. и доп. – М.: Высшая школа, 1981, – 288 с.
12. Приказ Министерства энергетики РФ от 3 августа 2018 г. № 630 «Методические указания по устойчивости энергосистем».
13. Тестовые схемы [Электронный ресурс] // URL: https://powersystem.info/index.php?title=Тестовые_схемы (дата обращения: 07.06.2020).
14. Официальный сайт Отдела энергетики Института социально-экономических и энергетических проблем Севера Коми научного центра Уральского отделения РАН [Электронный ресурс] // URL: http://energy.komisc.ru/downloads/schemes/ieee_14.txt (дата обращения: 07.06.2020).

Список литературы на английском языке / References in English

1. Idelchik V. I. Raschety ustanovivshihsya rezhimov elektricheskih sistem [Calculation of steady-state modes of electrical systems] / M.: Energy, 1977. – 192 p. [in Russian]
2. Ezhkov V. V. [Electrical systems and networks in examples and illustrations] / Ezhkov V. V., Zarudskij G. K., Zuev E. N. and other. M.: High School, 1999. – 352 p. [in Russian]
3. Chemborisova N. Sh. Obobshchennye pokazateli v zadachah upravleniya ustanovivshimisya rezhimami v raschetah elektroenergeticheskih sistem, Dissertaciya na soiskanie uchenoj stepeni doktora tekhnicheskih nauk [Generalized indicators in the problems of steady state control in the calculations of electric power systems, Thesis for the degree of PhD in Engineering] – Irkutsk, 2004. [in Russian]
4. Jerosolimski M. A new method for fast calculation of Jacobian matrices: automatic differentiation for power system simulation / Jerosolimski M., Levacher L. // IEEE Transactions on Power Systems, 9(2), pp. 700-706, 1994.
5. Zhang Y. P. Research on the relationship of the singular point for load flow jacobian matrix and the critical point of voltage collapse / Zhang Y, P., Huang W., Liu Z. Q., Yang J. Y., Cai X. L., Zhang J. H. IEEE Power Engineering Society General Meeting, 2005.
6. Naik S. D. On critical mode of bifurcation point and loadability in shunt compensated multi-bus power system / Naik S. D., Khedkar M. K., Bhat S. S. // International Conference on Power and Energy Systems, 2011.
7. Raja Masood Larik A statistical jacobian application for power system optimization of voltage stability / Raja Masood Larik, Mohd,Wazir Mustafa, Manoj Kumar Panjwani, 2019.
8. Yue Songa State-in-mode analysis of the power flow Jacobian for static voltage stability / Yue Songa, David J, Hilla, Tao Liua, 2019.
9. Chemborisova N. Sh. Ispol’zovanie modelej elementov seti i PK RASTR WIN pri raschetah i analize rezhimov EES: uchebnoe posobie po kursu “Primenenie EVM v elektroenergetike” po napravleniyu “Elektroenergetika i elektrotekhnika”, [Using models of network elements and RASTR WIN in calculations and analysis of power system regimes: a tutorial on the course “Computer Applications in the Power Engineering” in the direction “Power Engineering and Electrical Engineering”] / Chemborisova N. Sh., Burmejster M. V., Yusupov I. H. M.: Publishing House MPEI, 2018. – 68 p. [in Russian]
10. Nejumin V. G. Programmnyj kompleks «RastrWin3», Rukovodstvo pol’zovatelya [Software product «RastrWin3», User’s manual] / Nejumin V. G., Mashalov E. V., Aleksandrov A. S., Bagryancev A. A., 25.12.2018. [in Russian]
11. Venikov V. A. Elektricheskie sistemy. Matematicheskie zadachi elektroenergetiki: Uchebnik dlya studentov vuzov [Electrical systems. Mathematical Problems in Power Engineering: Textbook for university students – 2nd edition] – M.: High School, 1981. – 288 p. [in Russian]
12. Prikaz Ministerstva energetiki RF ot 3 avgusta 2018 g. № 630 “Metodicheskie ukazaniya po ustojchivosti energosistem” [Order of the Ministry of Energy of the Russian Federation dated August 3, 2018 No. 630 “Guidelines for the stability of power systems”] [in Russian]
13. Testovye skhemy [Test schemes] [Electronic resource] // URL: https://powersystem.info/index.php?title=Тестовые_схемы (accessed: June 6, 2020). [in Russian]
14. Oficial’nyj sajt Otdela energetiki Instituta social’no-ekonomicheskih i energeticheskih problem Severa Komi nauchnogo centra Ural’skogo otdeleniya RAN [The official website of the Energy Department of the Institute of Socio-Economic and Energy Problems of the North of the Komi Science Center of the Ural Branch of the Russian Academy of Sciences] [Electronic resource] // URL: http://energy.komisc.ru/downloads/schemes/ieee_14.txt (accessed: June 6, 2020). [in Russian]