ОБ АЛГОРИТМЕ ТАКСОНОМИИ В ЗАДАЧЕ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ | Опубликовать статью ВАК, elibrary (НЭБ)

Кулбараков М.А.

Магистрант, Сибирский федеральный университет

ОБ АЛГОРИТМЕ ТАКСОНОМИИ В ЗАДАЧЕ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ

Аннотация

Рассматривается задача технической диагностики. Для решения задачи диагностики целесообразно использовать алгоритм распознавания образов без учителя. Для настройки параметров алгоритма предлагается проводить предобработку данных.

Ключевые слова: таксономия, техническая диагностика, повышение качества.

Kulbarakov M.A.

Graduate student, Siberian Federal University

ABOUT TAXONOMY ALGORITHM TO THE PROBLEM OF TECHNICAL DIAGNOSTICS

Abstract

We consider the problem of technical diagnostics. To solve the problem of diagnosis is advisable to use an algorithm for pattern recognition without teacher. To adjust the parameters of the algorithm is proposed to carry out pre-processing of data.

Keywords: taxonomy, technical diagnostics, improving the quality.

Рассмотрим процессы, часто встречающиеся на практике и являющиеся предметом исследования в теории распознавания образов [1]. Типичным для задач технической диагностики, диагностики состояния технологического процесса или объекта, является наличие облачной структуры в пространстве признаков, определяющей тот или иной класс.

Пусть некоторое изделие может быть отнесено к той или иной категории качества в соответствии с требованиями ГОСТ, предъявляемым к техническим объектам, функционирование которых предполагает длительный срок эксплуатации без проведения текущего ремонта.

Это изделие характеризуется значениями вектора признаков , полученных в результате испытаний и может быть отнесена к одному из двух классов . Задача распознавания образов сводится к построению решающего правила на основе имеющейся обучающей выборки , где  указания учителя о принадлежности  к , s – объем выборки. На Рис. 1 это иллюстрируется для трехмерного вектора v, m=3. Элементы обучающей выборки  на рисунке не показаны из соображений простоты. В дальнейшем выборку наблюдений переменных  объемом  – будем обозначать .

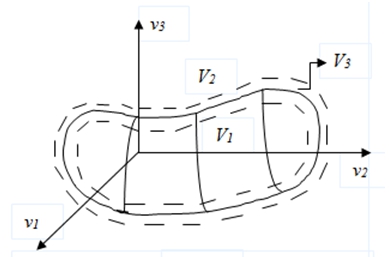
Рис. 1 – Иллюстрация задачи распознавания образов

 

Спецификой задач диагностики является то, что среди изделий присутствуют «очень хорошие» с точки зрения значений результатов испытаний, «хорошие» и «не очень хорошие». Бракованные изделия, не прошедшие испытания технические объекты в рамках ГОСТ или ТУ исключаются из выборки изделий. Количество классов может быть различным, но независимо от их числа обязательно присутствуют области перемешивания представителей соседних классов. Это изделия, меры принадлежности которых к каждому из двух соседних классов сравнимы по своим численным значениям. Такие детали представляют собой некую пограничную область между переходами из класса в класс, которая на рис.1 обозначена  − область перемешивания изделий разных классов. Можно сказать, что существует область, в которой расположены изделия, для которых  сложно определить, к какому именно из имеющихся классов они принадлежат. Это связано с тем, что расстояние между такими изделиями сравнительно мало и не дает оснований для однозначного вывода о принадлежности к определенной группе изделий.

Таким образом, возникает необходимость формулирования  задачи распознавания, с выделением пограничного класса изделий. Результаты диагностики следует в дальнейшем использовать для оптимизации технологического процесса производства технических объектов с целью уменьшения числа элементов пограничного класса.

Постановка задачи

Пусть имеется выборка изделий  объемом s, каждое из которых характеризуется значениями вектора признаков , полученных в результате испытаний. Рассмотрим задачу распознавания образов без учителя, в этом случае отсутствуют указания относительно количества классов или принадлежности изделия к тому или иному классу. Выборку изделий необходимо разделить на группы таким образом, чтобы элементы одной группы имели схожие значения признаков, а элементы разных групп отличилась друг от друга.

При эксплуатации ЭРИ в космических аппаратах нет возможности получить информацию о сроке службе, его поломке, поэтому нет сведений о дефектах, возникших в процессе эксплуатации. В этом случае целесообразно применять алгоритмы решения задачи таксономии [2].

Алгоритм решения задачи таксономии

На первоначальном этапе целесообразно провести нормирование и центрирование данных, для того чтобы привести значения к единому интервалу, т.к. шкалы измерения признаков  могут иметь различные значения. Затем происходит вычисление всех расстояний между объектами выборки с помощью выбранной метрики. В данном случае было взято Евклидово расстояние. Формула многомерного расстояния  между точками  имеет следующий вид:

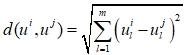    (1)

Для полученных расстояний строится гистограмма распределения. На гистограмме можно увидеть значение минимального и максимального расстояния между объектами.

Ниже представлен алгоритм группировки.

1. Из общего объема выборки s выделяем 20% точек, расстояния между которыми наименьшие. Если расстояние 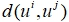 между точками  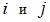 достаточно мало по сравнению с остальными, то такие точки принадлежат одному классу. В данную «малую» выборку могут попасть точки из нескольких групп.
2. Выделяем группы в «малой» выборке. Для этого берем произвольную точку и находим все точки из «малой» выборки, расстояния до которых меньше ∆₁, затем проделываем данную процедуру со всеми точками, попавшими в группу. После того, как будут найдены все точки, расстояния между которыми меньше ∆₁, объединяем их в группу. Далее эти точки исключаем из рассмотрения. Повторяем данную процедуру, пока все точки «малой» выборки не будут распределены по группам. Таким образом, мы получим группы, для каждой из которых находим центр. Координаты центра получаем как среднее арифметическое значений по каждому признаку всех точек группы.
3. Теперь рассмотрим оставшуюся выборку (80% точек от общего числа). Если расстояние от центра группы до точки выборки меньше ∆₂, то считаем, что точка принадлежит данной группе. Такую операцию проводим относительно каждого центра группы.
4. После разделения на группы могут остаться точки, которые не принадлежат ни одной из групп.

Таким образом, для решения задачи группировки с помощью предлагаемого алгоритма необходимо настроить два параметра группировки – ∆₁ и ∆₂. От величины параметр ∆₁ зависит конечное число групп, ∆₂ – радиус групп. Параметры должны удовлетворять следующему условию: минимальное значение расстояния (1) < ∆₁ < ∆₂ < максимальное значение расстояния.

Из соображения простоты на рис. 2 показан случай для двумерного вектора . В данном случае задача таксономии решается в двумерном пространстве, поэтому визуально легко поверить правильность решения задачи. На рис. 2 показаны точки выборки, где по оси абсцисс отложены значения параметра u₁, а по оси ординат – u₂. В результаты работы алгоритма было выделено три группы: они показаны на рис. 2 разными цветами, а также были точки, не принадлежащие ни одной из групп (отмечены квадратами).

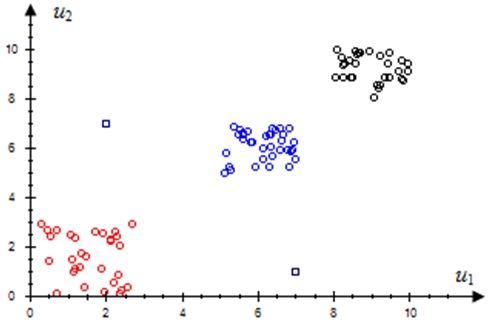
Рис. 2 – Пример работы алгоритма

 

Число классов может быть различным, однако всегда будут присутствовать точки, которые сложно отнести к какому-либо классу. Такие измерения могут возникнуть вследствие ошибки измерения.